
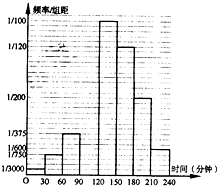
 为了调查学生星期天晚上学习时间利用问题,某校从高二年级1000名学生(其中走读生450名,住宿生550名)中,采用分层抽样的方法抽取n名学生进行问卷调查,根据问卷取得了这n名同学每天晚上学习时间(单位:分钟)的数据,按照以下区间分为八组①[0,30)②[30,60)③[60,90),④[90,120),⑤[120,150),⑥[150,180),⑦[180,210),⑧[210,240),得到频率分布直方图如下,已知抽取的学生中星期天晚上学习时间少于60分钟的人数为5人:
为了调查学生星期天晚上学习时间利用问题,某校从高二年级1000名学生(其中走读生450名,住宿生550名)中,采用分层抽样的方法抽取n名学生进行问卷调查,根据问卷取得了这n名同学每天晚上学习时间(单位:分钟)的数据,按照以下区间分为八组①[0,30)②[30,60)③[60,90),④[90,120),⑤[120,150),⑥[150,180),⑦[180,210),⑧[210,240),得到频率分布直方图如下,已知抽取的学生中星期天晚上学习时间少于60分钟的人数为5人:| 利用时间充分 | 利用时间不充分 | 总计 | |
| 走读生 | |||
| 住宿生 | 10 | ||
| 总计 |
分析 (1)由频率分布直方图求出学习时间少于60分钟的频率为$\frac{5}{100}$,从而求出n=100,求出第④组的频率,从而求出第④组的高度,进而能求出频率分布直方图如图.
(2)由频率分布直方图求出2×2列联表,从而得K2≈3.030<3.841,从而没有理由认为学生“利用时间是否充分”与走读、住宿有关.
(3)由题意X的所有可能取值为0,1,2,3,P(X=i)=$\frac{{C}_{5}^{i}{C}_{5}^{3-i}}{{C}_{10}^{3}}$,(i=0,1,2,3),由此能求出X的分布列和EX.
解答  (本小题满分12分)
(本小题满分12分)
解:(1)设第i组的频率为Pi(i=1,2,…,8),
由图可知:P1=$\frac{1}{3000}$×30=$\frac{1}{100}$,P2=$\frac{1}{750}$×30=$\frac{4}{100}$,
∴学习时间少于60分钟的频率为P1+P2=$\frac{5}{100}$
由题意:n×$\frac{5}{100}$=5∴n=100…(2分)
又P3=$\frac{1}{375}$×30=$\frac{8}{100}$,P5=$\frac{1}{100}$×30=$\frac{30}{100}$,
P6=$\frac{1}{120}$×30=$\frac{25}{100}$,P7=$\frac{1}{200}$×30=$\frac{15}{100}$,P8=$\frac{1}{600}$×30=$\frac{5}{100}$
∴P4=1-(P1+P2+P3+P5+P6+P7+P8)=$\frac{12}{100}$
∴第④组的高度为:h=$\frac{12}{100}$×$\frac{1}{30}$=$\frac{12}{3000}$=$\frac{1}{250}$
频率分布直方图如图.…(4分)
(2)由频率分布直方图可知,在抽取的100人中,
“走读生”有45人,利用时间不充分的有15人,
从而2×2列联表如下:
| 利用时间充分 | 利用时间不充分 | 总计 | |
| 走读生 | 30 | 15 | 45 |
| 住宿生 | 45 | 10 | 55 |
| 总计 | 75 | 25 | 100 |
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{12}$ | $\frac{5}{12}$ | $\frac{5}{12}$ | $\frac{1}{12}$ |
点评 本题考查概率的求法,考查独立性检验的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意超几何分布的性质的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | 4 | C. | $±\frac{1}{4}$ | D. | ±4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 焦距相等 | B. | 离心率相等 | C. | 焦点相同 | D. | 有相等的长、短轴 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
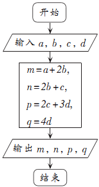
| A. | 4,6,1,7 | B. | 7,6,1,4 | C. | 1,6,4,7 | D. | 6,4,1,7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com