
分析 根据绝对值的定义,利用适当的方法去掉绝对值,化为整式方程,解方程即可.
解答 解:(1)∵3×|2x-1|-1=5,
∴3×|2x-1|=6,
∴|2x-1|=2,
∴2x-1=2或2x-1=-2,
解得x=$\frac{3}{2}$或x=-$\frac{1}{2}$;
(2)∵|x-|2x+1||=3,
∴x-|2x+1|=3或x-|2x+1|=-3,
即x-3=|2x+1|①或x+3=|2x+1|②,
解①得,x2-6x+9=4x2+4x+1,
解得x=-4(不合题意,舍去)或x=$\frac{2}{3}$(不合题意,舍去);
解②得,x2+6x+9=4x2+4x+1,
解得x=2或x=-$\frac{4}{3}$;
综上,原方程的解为x=2或x=-$\frac{4}{3}$;
(3)∵|x-2|+|x+5|=6,
∴当x≤-5时,方程化为-(x-2)-(x+5)=6,解得x=-$\frac{9}{2}$(不合题意,舍去);
当-5<x<2时,方程化为-(x-2)+(x+5)=6,此方程无解;
当x≥2时,方程化为(x-2)+(x+5)=6,解得x=$\frac{3}{2}$(不合题意,舍去);
综上,此方程无解;
(4)∴|x-5|+$\sqrt{(4-x)^{2}}$=1,
∴|x-5|+|x-4|=1;
∴当x≤4时,方程化为-(x-5)-(x-4)=1,解得x=4;
当4<x<5时,方程化为-(x-5)+(x-4)=1,解得4<x<5;
当x≥5时,方程化为(x-5)+(x-4)=1,解得x=5;
综上,原方程的解为4≤x≤5;
(5)∵x|x|-3|x|+2=0
∴当x≥0时,方程化为x2-3x+2=0,解得x=1或x=2;
当x<0时,方程化为-x2+3x+2=0,解得x=$\frac{3-\sqrt{17}}{2}$或x=$\frac{3+\sqrt{17}}{2}$(不合题意,舍去);
综上,原方程的解为x=1或x=2或x=$\frac{3-\sqrt{17}}{2}$.
点评 本题考查了含有绝对值的方程的解法与应用问题,解题的关键是去掉绝对值,是综合性题目.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
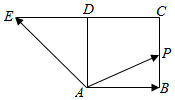 如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中 $\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AE}$,下列判断正确的是( )
如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中 $\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AE}$,下列判断正确的是( )| A. | 满足λ+μ=2的点P必为BC的中点 | B. | 满足λ+μ=1的点P有且只有一个 | ||
| C. | 满足λ+μ=a(a>0)的点P最多有3个 | D. | λ+μ的最大值为3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
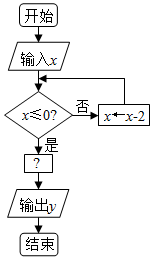 如图是一个算法的程序框图,当输入的x的值为7时,输出的y值恰好是-1,则“?”处应填的关系式可能是( )
如图是一个算法的程序框图,当输入的x的值为7时,输出的y值恰好是-1,则“?”处应填的关系式可能是( )| A. | y=2x+1 | B. | y=3-x | C. | y=|x| | D. | y=${log_{\frac{1}{3}}}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com