
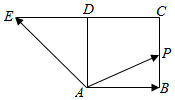
 如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中 $\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AE}$,下列判断正确的是( )
如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中 $\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AE}$,下列判断正确的是( )| A. | 满足λ+μ=2的点P必为BC的中点 | B. | 满足λ+μ=1的点P有且只有一个 | ||
| C. | 满足λ+μ=a(a>0)的点P最多有3个 | D. | λ+μ的最大值为3 |
分析 可分别以AB,AD所在直线为x轴,y轴,建立平面直角坐标系,并设正方形边长为1,P(x,y),x,y∈[0,1],可求A,B,E三点坐标,从而可写出向量$\overrightarrow{AP},\overrightarrow{AB},\overrightarrow{AE}$的坐标,带入$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$便可得到(x,y)=(λ-μ,μ),从而得到$λ+μ=\left\{\begin{array}{l}{x}&{y=0}\\{1+2y}&{x=1}\\{x+2}&{y=1}\\{2y}&{x=0}\end{array}\right.$,这样便可判断每个选项的正误,从而得出正确选项.
解答 解:以AB,AD所在直线分别为x,y轴,建立如图所示平面直角坐标系,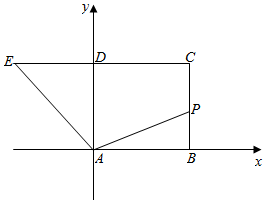
设正方形边长为1,P(x,y),则:
A(0,0),B(1,0),E(-1,1);
∴$\overrightarrow{AP}=(x,y),\overrightarrow{AB}=(1,0),\overrightarrow{AE}(-1,1)$;
∴由$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$得,(x,y)=(λ-μ,μ);
∴$λ+μ=x+2y=\left\{\begin{array}{l}{x}&{y=0}\\{1+2y}&{x=1}\\{x+2}&{y=1}\\{2y}&{x=0}\end{array}\right.$;
∴满足λ+μ=2的点P有线段BC的中点和D点;
满足λ+μ=1的点P有B点和线段AD的中点;
满足λ+μ=a(a>0)的点最多有2个;
x=1,y=1时,λ+μ取最大值3.
故选D.
点评 考查通过建立平面直角坐标系,利用坐标解决向量问题的方法,能求平面上点的坐标,根据点的坐标可求向量的坐标,以及向量数乘的坐标运算.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{f(e)}{e+1}$>$\frac{f(π)}{π+1}$ | B. | $\frac{f(e)}{e+1}$<$\frac{f(π)}{π+1}$ | C. | $\frac{f(e)}{e+2}$>$\frac{f(π)}{π+2}$ | D. | $\frac{f(e)}{e+2}$<$\frac{f(π)}{π+2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | $\sqrt{5}$ | C. | $\frac{9}{2}$ | D. | $\frac{{3\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-1) | B. | (1,2) | C. | (-1,+∞) | D. | (-ln2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com