
| A. | (-2,-1) | B. | (1,2) | C. | (-1,+∞) | D. | (-ln2,+∞) |
分析 先根据导数的几何意义写出函数f(x)在点A、B处的切线方程,再利用两直线重合的充要条件:斜率相等且纵截距相等,列出关系式,从而得出a=lnx2-$\frac{1}{4}$($\frac{1}{{x}_{2}}$-1)2-1,构造h(t)=-lnt+$\frac{1}{4}$t2-$\frac{1}{2}$t-$\frac{3}{4}$,(0<t<1),最后利用导数研究它的单调性和最值,即可得出a的取值范围.
解答 解:当x<0时,f(x)=x2+x+a的导数为f′(x)=2x+1;
当x>0时,f(x)=lnx的导数为f′(x)=$\frac{1}{x}$,
设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的两点,且x1<x2,
当x1<x2<0,或0<x1<x2时,f′(x1)≠f′(x2),故x1<0<x2,
当x1<0时,函数f(x)在点A(x1,f(x1))处的切线方程为
y-(x12+x1+a)=(2x1+1)(x-x1);
当x2>0时,函数f(x)在点B(x2,f(x2))处的切线方程为
y-lnx2=$\frac{1}{{x}_{2}}$(x-x2).
两直线重合的充要条件是$\frac{1}{{x}_{2}}$=2x1+1①,lnx2-1=-x12+a②,
由①及x1<0<x2得0<$\frac{1}{{x}_{2}}$<1,由①②得a=lnx2-$\frac{1}{4}$($\frac{1}{{x}_{2}}$-1)2-1,
令t=$\frac{1}{{x}_{2}}$,则0<t<1,且a=-lnt+$\frac{1}{4}$t2-$\frac{1}{2}$t-$\frac{3}{4}$,
设h(t)=-lnt+$\frac{1}{4}$t2-$\frac{1}{2}$t-$\frac{3}{4}$,(0<t<1)
则h′(t)=-$\frac{1}{t}$+$\frac{1}{2}$t-$\frac{1}{2}$<0,即h(t)在(0,1)为减函数,
则h(t)>h(1)=-ln1-1=-1,
则a>-1,
可得函数f(x)的图象在点A,B处的切线重合,
a的取值范围是(-1,+∞).
故选:C.
点评 本题主要考查了导数的几何意义等基础知识,考查了推理论证能力、运算能力、创新意识,考查了函数与方程、分类与整合、转化与化归等思想方法.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
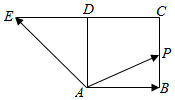 如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中 $\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AE}$,下列判断正确的是( )
如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中 $\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AE}$,下列判断正确的是( )| A. | 满足λ+μ=2的点P必为BC的中点 | B. | 满足λ+μ=1的点P有且只有一个 | ||
| C. | 满足λ+μ=a(a>0)的点P最多有3个 | D. | λ+μ的最大值为3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
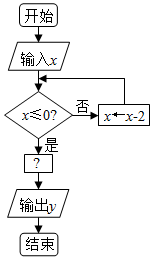 如图是一个算法的程序框图,当输入的x的值为7时,输出的y值恰好是-1,则“?”处应填的关系式可能是( )
如图是一个算法的程序框图,当输入的x的值为7时,输出的y值恰好是-1,则“?”处应填的关系式可能是( )| A. | y=2x+1 | B. | y=3-x | C. | y=|x| | D. | y=${log_{\frac{1}{3}}}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com