
分析 根据正项数列{an},以及an2≤an-an+1,可得0<an+1≤an-an2,解此不等式即可得到0<an<1,不难得出a1<1,a2<1,利用数学归纳法证明即可利用数学归纳法证明即可.
解答 解:an2≤an-an+1,得an+1≤an-an2
∵在数列{an}中an>0,
∴an+1>0,
∴an-an2>0,
∴0<an<1,
∴a2≤a1-a12=a1(1-a1)≤($\frac{{a}_{1}+1-{a}_{1}}{2}$)2=$\frac{1}{4}$<$\frac{1}{2}$
由此猜想:an<$\frac{1}{n}$(n≥2).下面用数学归纳法证明:
①当n=2时,显然成立;
②当n=k时(k≥2,k∈N)时,假设猜想正确,即ak<$\frac{1}{k}$
那么ak+1≤ak-ak2=-(ak-$\frac{1}{2}$)2+$\frac{1}{4}$≤-($\frac{1}{k}$-$\frac{1}{2}$)2+$\frac{1}{4}$=$\frac{1}{k}$-$\frac{1}{{k}^{2}}$=$\frac{k-1}{{k}^{2}}$<$\frac{k-1}{{k}^{2}-1}$<$\frac{1}{k+1}$
∴当n=k+1时,猜想也正确
综上所述,对于一切n∈N*,an<$\frac{1}{n}$.
点评 本题主要考查数列与不等式问题和数学归纳法,对探究性问题先归纳,再猜想,最后利用数学归纳法证明,数学归纳法的关键是递推环节,要符合假设的模型才能成立,属中档题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
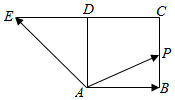 如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中 $\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AE}$,下列判断正确的是( )
如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中 $\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AE}$,下列判断正确的是( )| A. | 满足λ+μ=2的点P必为BC的中点 | B. | 满足λ+μ=1的点P有且只有一个 | ||
| C. | 满足λ+μ=a(a>0)的点P最多有3个 | D. | λ+μ的最大值为3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com