
| A�� | $\frac{f��e��}{e+1}$��$\frac{f����}{��+1}$ | B�� | $\frac{f��e��}{e+1}$��$\frac{f����}{��+1}$ | C�� | $\frac{f��e��}{e+2}$��$\frac{f����}{��+2}$ | D�� | $\frac{f��e��}{e+2}$��$\frac{f����}{��+2}$ |
���� ��������������f�䣨x����0�����ݸ��Ϻ�������f�䣨x-1��=f�䣨x����0����$\frac{f��x-1��}{f�䣨x-1��}$��x�������ã�$\frac{f��x-1��-xf�䣨x-1��}{f�䣨x-1��}$��0�����Եõ�f��x-1��-xf�䣨x-1����0�����츨��������g��x��=$\frac{f��x-1��}{x}$��x��0��������ʽ��֪g�䣨x����0��g��x�������������Դ˿����ж�$\frac{f��e��}{f��e+1��}$��$\frac{f���У�}{f����+1��}$��
��� �⣺y=f��x��Ϊ�������ϵĵ�������������
�࣬y=f�䣨x����0��
$\frac{f��x-1��}{f�䣨x-1��}$��x����$\frac{f��x-1��}{f�䣨x-1��}$-x��0��
�����ã�$\frac{f��x-1��-xf�䣨x-1��}{f�䣨x-1��}$��0��
�ɸ��Ϻ��������֪��f�䣨x-1��=f�䣨x����0��
��f��x-1��-xf�䣨x-1����0��
��g��x��=$\frac{f��x-1��}{x}$��x��0��
g�䣨x��=$\frac{xf�䣨x-1��-f��x-1��}{{x}^{2}}$��
��xf�䣨x-1��-f��x-1����0��
��g�䣨x����0��
��g��x������������
��e+1����+1��
��$\frac{f��e��}{f��e+1��}$��$\frac{f����}{f����+1��}$��
�ʴ�ѡ��B��
���� ���⿼�����ú����ĵ����жϺ����ĵ������漰�˸��Ϻ������Լ����캯�����жϺ��������ԣ������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
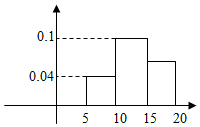
| A�� | 12 | B�� | 12.5 | C�� | 13 | D�� | 13.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
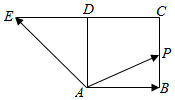 ��ͼ���ı���ABCD�������Σ��ӳ�CD��E��ʹ��DE=CD��������P�ӵ�A�������������εı߰���ʱ�뷽���˶�һ�ܻص�A�㣬���� $\overrightarrow{AP}$=��$\overrightarrow{AB}$+��$\overrightarrow{AE}$�������ж���ȷ���ǣ�������
��ͼ���ı���ABCD�������Σ��ӳ�CD��E��ʹ��DE=CD��������P�ӵ�A�������������εı߰���ʱ�뷽���˶�һ�ܻص�A�㣬���� $\overrightarrow{AP}$=��$\overrightarrow{AB}$+��$\overrightarrow{AE}$�������ж���ȷ���ǣ�������| A�� | �����+��=2�ĵ�P��ΪBC���е� | B�� | �����+��=1�ĵ�P����ֻ��һ�� | ||
| C�� | �����+��=a��a��0���ĵ�P�����3�� | D�� | ��+�̵����ֵΪ3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
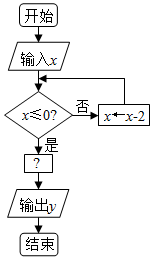 ��ͼ��һ���㷨�ij����ͼ���������x��ֵΪ7ʱ�������yֵǡ����-1��������Ӧ��Ĺ�ϵʽ�����ǣ�������
��ͼ��һ���㷨�ij����ͼ���������x��ֵΪ7ʱ�������yֵǡ����-1��������Ӧ��Ĺ�ϵʽ�����ǣ�������| A�� | y=2x+1 | B�� | y=3-x | C�� | y=|x| | D�� | y=${log_{\frac{1}{3}}}$x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com