
分析 求出M(2,2),设P(a,a),Q(x,$\frac{4}{x}$),根据PQ≥PM恒成立列出恒等式,利用基本不等式的性质讨论a,得出a的取值范围.
解答 解:解方程组$\left\{\begin{array}{l}{y=x}\\{y=\frac{4}{x}}\\{x>0}\end{array}\right.$得M(2,2).
设P(a,a),Q(x,$\frac{4}{x}$).则PQ=$\sqrt{(x-a)^{2}+(\frac{4}{x}-a)^{2}}$,PM=$\sqrt{2(a-2)^{2}}$.
∴(x-a)2+($\frac{4}{x}-a$)2≥2(a-2)2恒成立,
整理得:x2+$\frac{16}{{x}^{2}}$-2ax-$\frac{8a}{x}$≥8-8a恒成立.
∵x2+$\frac{16}{{x}^{2}}$$≥2\sqrt{16}=8$,
∴2ax+$\frac{8a}{x}$≤8a恒成立.
显然a=0时,上时恒成立.
若a>0,则2ax+$\frac{8a}{x}$≤8a恒成立?2x+$\frac{8}{x}$≤8恒成立,与2x+$\frac{8}{x}$≥2$\sqrt{2x•\frac{8}{x}}$=8矛盾.
若a<0,则2ax+$\frac{8a}{x}$≤8a恒成立?2x+$\frac{8}{x}$≥8恒成立,而2x+$\frac{8}{x}$≥2$\sqrt{2x•\frac{8}{x}}$=8恒成立.
∴a≤0.
故答案为(-∞,0].
点评 本题考查了利用基本不等式解决恒成立问题,距离公式,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$<a≤-1 | B. | a≤-$\frac{3}{2}$ | C. | a≤-1 | D. | a>-$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{f(e)}{e+1}$>$\frac{f(π)}{π+1}$ | B. | $\frac{f(e)}{e+1}$<$\frac{f(π)}{π+1}$ | C. | $\frac{f(e)}{e+2}$>$\frac{f(π)}{π+2}$ | D. | $\frac{f(e)}{e+2}$<$\frac{f(π)}{π+2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
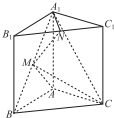 如图,在正三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠BAC=90°,AB=AC=AA1,点M,N分别为A1B和B1C1的中点.
如图,在正三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠BAC=90°,AB=AC=AA1,点M,N分别为A1B和B1C1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com