
���� �����յ���ʽ����������ʽ����f��2-x��=f��x��˵������ȷ������f��x���Ķ�������R������ͼ���жԳ��ᣬ�ɺ�������ʽ���Եó�����ͼ�������Դ���X�ᣬ���ڷ�ĸ��������ͼ�����������춼��������X�ᣬ˵�������������ں������ڴ����ɺ�������ʽ���������ͼ��Ĵ�����״��˵������ȷ���ܴ���
���  �⣺f��x��=$\frac{cos����x-�У�}{{2}^{x}+{2}^{2-x}}$=$\frac{-cos��x}{{2}^{x}+{2}^{2-x}}$��
�⣺f��x��=$\frac{cos����x-�У�}{{2}^{x}+{2}^{2-x}}$=$\frac{-cos��x}{{2}^{x}+{2}^{2-x}}$��
��f��2-x��=$\frac{-cos�У�2-x��}{{2}^{2-x}+{2}^{x}}=\frac{-cos��x}{{2}^{x}+{2}^{2-x}}=f��x��$���ຯ��f��x����ͼ��һ������ֱ��x=1�Գƣ��ʢ���ȷ��
��x��+��ʱ��2x+22-x��+�ޣ���f��x����0���ຯ��f��x����R�ϲ������ں������ʢڴ���
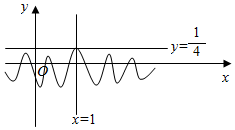
�ɢ�֪������f��x������ֱ��x=1�Գƣ��ҵ�x��1ʱ������x��������ͼ�������״��ͼ��
����f��x�������ֵΪ$\frac{1}{4}$���ʢ���ȷ��
��ͼ��֪����x=1�Ҳ�������������������б��С��0���ʢܴ���
�����������������Ǣ٢ۣ�
�ʴ�Ϊ���٢ۣ�
���� ���⿼�����Ǻ����еĺ�ȱ任Ӧ�ã������˺�����ͼ���ɺ�������ʽ���������ͼ��Ĵ�����״�ǽ�����Ĺؼ������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 1 | C�� | 2-2�� | D�� | 2��-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ����������ABC-A��B��C���У�D��E��F�ֱ�Ϊ��BC��A��A��AC���е㣮
����������ABC-A��B��C���У�D��E��F�ֱ�Ϊ��BC��A��A��AC���е㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com