
分析 (Ⅰ)求出f(x)的导数,通过讨论a的范围,得到导函数的符号,求出函数的单调区间即可;
(Ⅱ)要使方程f(x)=mx在区间[1,e2]上有唯一实数解,只需m=$\frac{lnx}{x}$-1有唯一实数解,令g(x)=$\frac{lnx}{x}$-1,(x>0),根据函数的单调性求出m的范围即可.
解答 解:( I)f′(x)=$\frac{(ax-1)(x-1)}{x}$,(x>0),(1分)
( i)当a=0时,f′(x)=$\frac{1-x}{x}$,令f′(x)>0,得0<x<1,令f′(x)<0,得x>1,
函数f(x)在(0,1)上单调递增,(1,+∞)上单调递减; (2分)
( ii)当0<a<1时,令f′(x)=0,得x1=1,x2=$\frac{1}{a}$>1 (3分)
令f′(x)>0,得0<x<1,x>$\frac{1}{a}$,令f′(x)<0,得1<x<$\frac{1}{a}$,
函数f(x)在(0,1)和($\frac{1}{a}$,+∞)上单调递增,(1,$\frac{1}{a}$)上单调递减; (4分)
( iii)当a=1时,f′(x)≥0,函数f(x)在(0,+∞)上单调递增;(5分)
( iv)当a>1时,0<$\frac{1}{a}$<1 (6分)
令f′(x)>0,得0<x<$\frac{1}{a}$,x>1,令f′(x)<0,得$\frac{1}{a}$<x<1,(7分)
函数f(x)在(0,$\frac{1}{a}$)和(1,+∞)上单调递增,($\frac{1}{a}$,1)上单调递减; (8分)
综上所述:当a=0时,函数f(x)的单调递增区间为(0,1),单调递减区间为(1,+∞);
当0<a<1时,函数f(x)的单调递增区间为(0,1)和($\frac{1}{a}$,+∞),单调递减区间为(1,$\frac{1}{a}$);
当a=1时,函数f(x)的单调递增区间为(0,+∞);
当a>1时,函数f(x)的单调递增区间为(0,$\frac{1}{a}$)和(1,+∞),单调递减区间为($\frac{1}{a}$,1)(9分)
( II)当a=0时,f(x)=-x+lnx,由f(x)=mx,得-x+lnx=mx,又x>0,所以m=$\frac{lnx}{x}$-1,
要使方程f(x)=mx在区间[1,e2]上有唯一实数解,
只需m=$\frac{lnx}{x}$-1有唯一实数解,(10分)
令g(x)=$\frac{lnx}{x}$-1,(x>0),∴g′(x)=$\frac{1-lnx}{{x}^{2}}$,
由g′(x)>0得0<x<e;g′(x)<0得x>e,
∴g(x)在区间[1,e]上是增函数,在区间[e,e2]上是减函数.(11分)
g(1)=-1,g(e)=$\frac{1}{e}$-1,g(e2)=$\frac{2}{{e}^{2}}$-1,
故-1≤m<$\frac{2}{{e}^{2}}$-1或m=$\frac{1}{e}$-1 (12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,是一道中档题.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
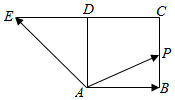 如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中 $\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AE}$,下列判断正确的是( )
如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中 $\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AE}$,下列判断正确的是( )| A. | 满足λ+μ=2的点P必为BC的中点 | B. | 满足λ+μ=1的点P有且只有一个 | ||
| C. | 满足λ+μ=a(a>0)的点P最多有3个 | D. | λ+μ的最大值为3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=-xe|x| | B. | f(x)=x+sinx | ||
| C. | f(x)=$\left\{\begin{array}{l}{lg(x+1),x≥0}\\{lg(1-x),x<0}{\;}\end{array}\right.$ | D. | f(x)=x2|x| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com