
【题目】已知函数![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 只有一个零点
只有一个零点![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根据导数的几何意义求出切线的斜率,然后由点斜式可得所求切线方程.(2)利用导数判断出函数![]() 的单调性和极值,进而得到函数
的单调性和极值,进而得到函数![]() 的大体图象,然后根据函数的图象及极值判断出函数只有一个零点时参数
的大体图象,然后根据函数的图象及极值判断出函数只有一个零点时参数![]() 的取值范围.
的取值范围.
(1)当![]() 时,
时,![]() ,
,
所以![]() ,
,
故![]() ,
,
又![]() ,
,
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]() .
.
(2)由题意得![]() .
.
(i)当![]() ,即
,即![]() 时,
时,
则当![]() 或
或![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以![]() 的极小值为
的极小值为![]() ,
,
因为函数的零点![]() ,且
,且![]() ,
,
所以当函数只有一个零点时,需满足![]() ,
,
又![]() ,则
,则![]() 或
或![]() .
.
(ii)当![]() ,即
,即![]() 时,则有
时,则有![]() ,
,
所以![]() 为增函数.
为增函数.
又![]() ,
,
所以![]() 只有一个零点
只有一个零点![]() ,且
,且![]() ,
,
所以![]() 满足题意.
满足题意.
(iii)当![]() ,即
,即![]() 时,
时,
则当![]() 或
或![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() 的极小值为
的极小值为![]() ,极大值为
,极大值为![]() ,
,
因为![]() ,
,![]() ,
,
所以![]() ,
,
又![]() ,所以
,所以![]() .
.
综上可得![]() 或
或![]() .
.
实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρ(1-cos2θ)=8cosθ,直线ρcosθ=1与曲线C相交于M,N两点,直线l过定点P(2,0)且倾斜角为α,l交曲线C于A,B两点.
(1)把曲线C化成直角坐标方程,并求|MN|的值;
(2)若|PA|,|MN|,|PB|成等比数列,求直线l的倾斜角α.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面![]() 平面
平面![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,四边形
,四边形![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
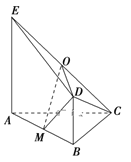
(1求异面直角![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,左焦点为
,左焦点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上位于
上位于![]() 轴上方的一个动点,当直线
轴上方的一个动点,当直线![]() 的斜率为1时,
的斜率为1时,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 的另外一个交点为
的另外一个交点为![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为降低汽车尾气排放量,某工厂设计制造了![]() 、
、![]() 两种不同型号的节排器,规定性能质量评分在
两种不同型号的节排器,规定性能质量评分在![]() 的为优质品.现从该厂生产的
的为优质品.现从该厂生产的![]() 、
、![]() 两种型号的节排器中,分别随机抽取500件产品进行性能质量评分,并将评分分别分成以下六个组;
两种型号的节排器中,分别随机抽取500件产品进行性能质量评分,并将评分分别分成以下六个组;![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,绘制成如图所示的频率分布直方图:
,绘制成如图所示的频率分布直方图:
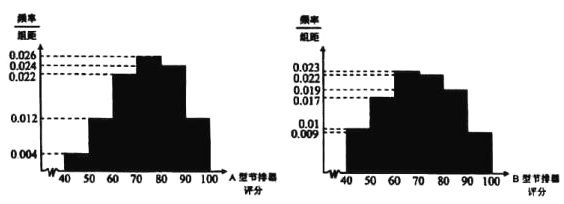
(1)设500件![]() 型产品性能质量评分的中位数为
型产品性能质量评分的中位数为![]() ,直接写出
,直接写出![]() 所在的分组区间;
所在的分组区间;
(2)请完成下面的列联表(单位:件)(把有关结果直接填入下面的表格中);
|
| 总计 | |
优质品 | |||
非优质品 | |||
总计 | 500 | 500 | 1000 |
(3)根据(2)中的列联表,能否有![]() 的把握认为
的把握认为![]() 、
、![]() 两种不同型号的节排器性能质量有差异?
两种不同型号的节排器性能质量有差异?
附:![]() ,其中
,其中![]() .
.
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
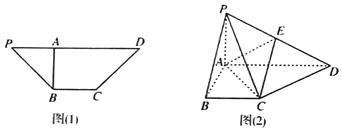
【题目】如图![]() 在四边形PBCD中,
在四边形PBCD中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,沿AB把三角形PAB折起,使P,D两点的距离为10,得到如图
,沿AB把三角形PAB折起,使P,D两点的距离为10,得到如图![]() 所示图形.
所示图形.
![]() Ⅰ
Ⅰ![]() 求证:平面
求证:平面![]() 平面PAC;
平面PAC;
![]() Ⅱ
Ⅱ![]() 若点E是PD的中点,求三棱锥
若点E是PD的中点,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com