
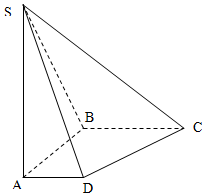
 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$.
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$.分析 (1),由题设条四棱锥S-ABCD的体积:V=$\frac{1}{3}$Sh=$\frac{1}{3}$×$\frac{1}{2}$×(AD+BC)×AB×SA,即可求得四棱锥S-ABCD的体积;
(2),由SA⊥面ABCD,知SA⊥BC,由AB⊥BC,BC⊥面SAB,由此能够证明面SAB⊥面SBC;
(3),连接AC,知∠SCA 就是SC与底面ABCD所成的角,由此能求出 SC与底面ABCD所成角的正切值.
解答 解:(1)∵底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$.
∴四棱锥S-ABCD的体积:V=$\frac{1}{3}$Sh=$\frac{1}{3}$×$\frac{1}{2}$×(AD+BC)×AB×SA=$\frac{1}{6}$×($\frac{1}{2}$+1)×1×1=$\frac{1}{4}$.
(2)证明:∵SA⊥面ABCD,BC?面ABCD,
∴SA⊥BC,
∵AB⊥BC,SA∩AB=A,
∴BC⊥面SAB.
∵BC?面SBC,
∴面SAB⊥面SBC.
(3)连接AC,
∵SA⊥面ABCD,
∴∠SCA 就是SC与底面ABCD所成的角.
在三角形SCA中,
∵SA=1,AC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∴tan∠SCA=$\frac{SA}{AC}$=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$
点评 本题考查棱锥的体积公式,考查直线与平面所成角的求法,平面与平面垂直的判定定理的应用,考查空间想象能力以及计算能力,属于中档题.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:选择题
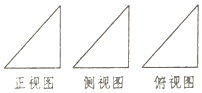
| A. | $\frac{3}{2}π$ | B. | $\sqrt{3}π$ | C. | $\frac{{\sqrt{3}}}{2}π$ | D. | 3π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若p∨q为真命题,则p∧q为真命题 | |
| B. | “x>5”是“x2-4x-5>0”的充分不必要条件 | |
| C. | 命题p:?x0∈R,x02+x0-1<0,则?p:?x∈R,x2+x-1≥0 | |
| D. | 命题“若x2-3x+2=0,则x=1或x=2”的逆否命题为“若x≠1且x≠2,则x2-3x+2≠0” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
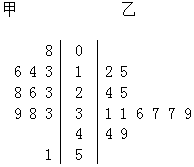
| A. | 26 33.5 | B. | 26 36 | C. | 23 31 | D. | 24.5 33.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com