练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．函数f（x）=x3+4x+9的图象在x=1处的切线在x轴上的截距为（　　）
    A．7B．1C．-1D．-7

    分析 欲求在点x=1处的切线方程，只须求出其斜率的值即可，故先利用导数求出在x=1处的导函数值，再结合导数的几何意义即可求出切线的斜率得到直线方程，最后令即可求得在x轴上的截距．从而问题解决．

    解答 解：∵f（x）=x3+4x+9，
    ∴f'（x）=3x2+4，当x=1时，y'=7得切线的斜率为7，所以k=7；
    所以曲线在点（1，14）处的切线方程为：
    y-14=7×（x-1），令y=0得x=-1．
    函数f（x）=x3+4x+9的图象在x=1处的切线在x轴上的截距为：-1．
    故选：C．

    点评 本小题主要考查直线的斜率、直线的方程、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识，考查运算求解能力．属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

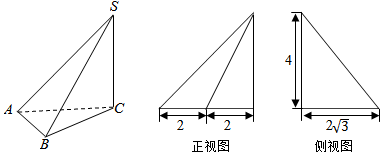
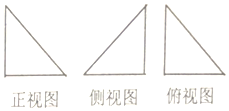    19．一几何体的三视图如图所示，三个三角形都是直角边为2的等腰直角三角形，该几何体的顶点都在球O上，球O的表面积为（　　）
    A．16πB．3πC．$4\sqrt{3}π$D．12π

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知函数$\begin{array}{l}\\ f（x）={x^2}-2x+2，x∈[{-2，2}]\end{array}$
    （1）求函数的顶点坐标   
    （2）求y=f（x）在区间[-2，2]上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．三棱锥S-ABC及其三视图中的正视图和侧视图如图所示，则棱SB的长为4$\sqrt{2}$；直线SB与AC所成角的余弦值为$\frac{\sqrt{2}}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知直线l：ax+（1-2a）y+1-a=0则直线恒过定点（-1，-1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知函数f（x）=$\frac{1+lnx}{x}$在区间（a，a+$\frac{2}{3}$）（a＞0）上不单调，则实数a的取值范围是（　　）
    A．（0，1）B．（$\frac{2}{3}$，1）C．（$\frac{1}{2}$，1）D．（$\frac{1}{3}$，1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

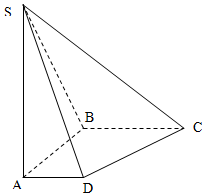    1．如图，在底面是直角梯形的四棱锥S-ABCD中，∠ABC=90°，SA⊥面ABCD，SA=AB=BC=1，AD=$\frac{1}{2}$．
    （1）求四棱锥S-ABCD的体积；
    （2）求证：BC⊥面SAB；
    （3）求SC与底面ABCD所成角的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

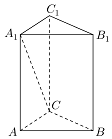    18．如图，已知正三棱柱ABC-A1B1C1的底面积为$\frac{{9\sqrt{3}}}{4}$，侧面积为36；
    （1）求正三棱柱ABC-A1B1C1的体积；
    （2）求异面直线A1C与AB所成的角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知奇函数f（x）是定义在R上的增函数，数列{xn}是一个公差为2的等差数列，满足f（x7）+f（x8）=0，则x2017的值为4019．

    查看答案和解析>>

    同步练习册答案