练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    要在墙上开一个上半部为半圆形、下部为矩形的窗户(如图所示)，在窗框为定长的条件下，要使窗户能够透过最多的光线，窗户应设计成怎样的尺寸？


    解： 设半圆直径为2R, 矩形的高为a，

    则2a＋2R＋πR＝L(定值)，

    S＝2Ra＋πR2＝－R2＋LR，

    当R＝时S最大，此时＝1，

    即半圆直径与矩形的高的比为2∶1时，窗户能够透过最多的光线．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    圆C的方程为x2+y2-2x-2y-2=0，则该圆的半径，圆心坐标分别为

    A . 2，（-2，1）   B . 4，（1，1）   C.2，（1，,1）    D .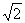，（1，2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    双曲线的焦距是（　　）

    A．8            B．4             C．            D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数，

    （1）求在点（1,0）处的切线方程；

    （2）判断及在区间上的单调性；

    （3）证明：在上恒成立

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知关于x的不等式：<1.

    (1) 当a＝1时，解该不等式；

    (2) 当a>0时，解该不等式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    甲厂以x千克/小时的速度运输生产某种产品(生产条件要求1≤x≤10)，每小时可获得利润是100(5x＋1－)元．

    (1) 要使生产该产品2小时获得的利润不低于3 000元，求x的取值范围；

    (2) 要使生产900千克该产品获得的利润最大，问：甲厂应该选取何种生产速度？并求最大利润．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     已知实数x、y满足则z＝2x＋y的最小值是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某营养师要为某个儿童预订午餐和晚餐．已知一个单位的午餐含12个单位的碳水化合物、6个单位的蛋白质和6个单位的维生素C；一个单位的晚餐含8个单位的碳水化合物、6个单位的蛋白质和10个单位的维生素C.另外，该儿童这两餐需要的营养中至少含64个单位的碳水化合物、42个单位的蛋白质和54个单位的维生素C.

    如果一个单位的午餐、晚餐的费用分别是2.5元和4元，那么要满足上述的营养要求，并且花费最少，应当为该儿童分别预订多少个单位的午餐和晚餐？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用0到9这10个数字，可以组成多少个没有重复数字的三位数？

    查看答案和解析>>

    同步练习册答案