
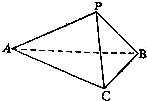
分析 由三棱锥的各面全等可知三棱锥可看做长方体切去四个小棱锥得到的,长方体的面对角线为13,14,15,求出长方体的棱长,使用作差法求出体积.
解答 解:由题意可知三棱锥的四个面全等.
故三棱锥可看做是对角线为13,14,15的长方体的面对角线组成的棱锥.
设长方体的棱长分别为a,b,c,则$\left\{\begin{array}{l}{{a}^{2}+{b}^{2}=169}\\{{a}^{2}+{c}^{2}=196}\\{{b}^{2}+{c}^{2}=225}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}^{2}=70}\\{{b}^{2}=99}\\{{c}^{2}=126}\end{array}\right.$.
∴长方体的体积V长方体=abc=$\sqrt{{a}^{2}{b}^{2}{c}^{2}}$=126$\sqrt{55}$.
∴三棱锥的体积为V=V长方体-4×$\frac{1}{3}×\frac{1}{2}abc$=$\frac{1}{3}{V}_{长方体}$=42$\sqrt{55}$.
点评 本题考查了棱锥的体积计算,发现棱锥的特点是解题关键,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
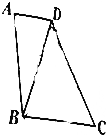 在直角梯形ABCD中,AD∥BC,∠A=90°,AB=2AD,若将△ABD沿直线BD折成△A′BD,使得A′D⊥BC,则直线A′B与平面BCD所成角的正弦值是$\frac{\sqrt{3}}{4}$.
在直角梯形ABCD中,AD∥BC,∠A=90°,AB=2AD,若将△ABD沿直线BD折成△A′BD,使得A′D⊥BC,则直线A′B与平面BCD所成角的正弦值是$\frac{\sqrt{3}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
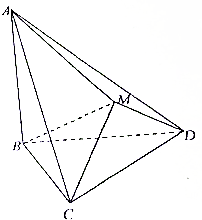 如图,△BCD与△MCD都是正三角形,平面MCD⊥平面BCD,AB⊥平面BCD.
如图,△BCD与△MCD都是正三角形,平面MCD⊥平面BCD,AB⊥平面BCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com