
分析 直接利用向量的坐标运算求解即可.
解答 解:不共线的两个向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$,设向量$\overrightarrow{a}$=3$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$,$\overrightarrow{b}$=$\overrightarrow{{e}_{2}}$-2$\overrightarrow{{e}_{1}}$,
则($\frac{1}{3}$$\overrightarrow{a}$+$\overrightarrow{b}$)+($\overrightarrow{a}$-$\frac{3}{2}$$\overrightarrow{b}$)+(2$\overrightarrow{b}$-$\overrightarrow{a}$)=$\frac{1}{3}\overrightarrow{a}$+$\frac{3}{2}\overrightarrow{b}$=$\frac{1}{3}$(3$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$)+$\frac{3}{2}$($\overrightarrow{{e}_{2}}$-2$\overrightarrow{{e}_{1}}$)
=-2$\overrightarrow{{e}_{1}}$+$\frac{5}{6}\overrightarrow{{e}_{2}}$,
故答案为:-2$\overrightarrow{{e}_{1}}$+$\frac{5}{6}\overrightarrow{{e}_{2}}$.
点评 本题考查平面向量的加减运算,考查计算能力.


 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\frac{1}{|x|}$ | B. | $f(x)={(\frac{1}{3})^x}$ | C. | f(x)=x2+1 | D. | f(x)=lg|x| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{1}{2},+∞})$ | B. | ($\frac{1}{2}$,+∞) | C. | [2,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
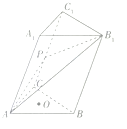 如图所示,在三棱锥ABC-A1B1C1中,底面△ABC为边长为6的等边三角形,点A1在平面ABC内的射影为△ABC的中心.
如图所示,在三棱锥ABC-A1B1C1中,底面△ABC为边长为6的等边三角形,点A1在平面ABC内的射影为△ABC的中心.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
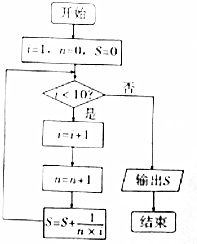
| A. | $\frac{7}{8}$ | B. | $\frac{8}{9}$ | C. | $\frac{9}{10}$ | D. | $\frac{10}{11}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com