
| A. | $\frac{7}{8}$ | B. | $\frac{8}{9}$ | C. | $\frac{9}{10}$ | D. | $\frac{10}{11}$ |
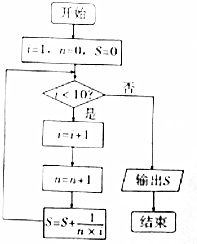
分析 每个循环的S值可按规律写出结果,也可用数列裂项相消法求解,即S=$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+…+\frac{1}{9×10}$=$1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{9}-\frac{1}{10}$=$1-\frac{1}{10}$=$\frac{9}{10}$
解答 初始条件:i=1,n=0,S=0,
进入第一次终止条件判断:1<10?选择是,
则$i=2,\;\;n=1,\;\;S=\frac{1}{1×2}$=$\frac{1}{2}$;
进入第二次终止条件判断:2<10?选择是,
则$i=3,\;\;n=2,\;\;S=\frac{1}{1×2}+\frac{1}{2×3}$=$\frac{2}{3}$;
进入第三次终止条件判断:3<10?选择是,
则$i=4,\;\;n=3,\;\;S=\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}$=$\frac{3}{4}$;
依此下去,
进入第九次终止条件判断:9<10?选择是,
则i=10,n=9,S=$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+…+\frac{1}{9×10}$=$\frac{9}{10}$;
进入第十次终止条件判断:10<10?选择否,
则输出S=$\frac{9}{10}$.
故选:C.
点评 考查算法和程序框图中循环结构,考查了数列的裂项相消法求和或数列的规律性.有知识点的综合,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3) | B. | (2,4) | C. | (3,5) | D. | (4,6) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
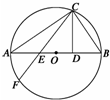 如图,AB是圆O的直径,CD⊥AB于D,且AD=2BD,E为AD的中点,连接CE并延长交圆O于F.若CD=$\sqrt{2}$,则求线段AB与EF的长度.
如图,AB是圆O的直径,CD⊥AB于D,且AD=2BD,E为AD的中点,连接CE并延长交圆O于F.若CD=$\sqrt{2}$,则求线段AB与EF的长度.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
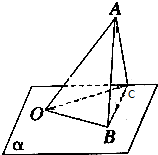 如图所示,已知∠BOC在平面α内,OA是平面α的斜线,且∠AOB=∠AOC=60°,OA=OB=OC=a,BC=$\sqrt{2}$a,求OA和平面α所成的角.
如图所示,已知∠BOC在平面α内,OA是平面α的斜线,且∠AOB=∠AOC=60°,OA=OB=OC=a,BC=$\sqrt{2}$a,求OA和平面α所成的角.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com