
分析 解不等式求出集合A,B,
(1)若A⊆B,则$\left\{\begin{array}{l}2≤a\\ 3a≥4\end{array}\right.$,可得a的取值范围;
(2)若A∩B={x|3<x<4},则a=3.
解答 解:(1)集合A={x|x2-6x+8<0}=(2,4),
B={x|(x-a)(x-3a)<0}=(a,3a),a>0,
若A⊆B,则$\left\{\begin{array}{l}2≤a\\ 3a≥4\end{array}\right.$
解得:$\frac{4}{3}$≤a≤2.
(2)若A∩B={x|3<x<4},
则a=3.
点评 本题考查的知识点是集合包含关系判断及应用,集合的交集运算,难度不大,属于基础题.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{1}{2},+∞})$ | B. | ($\frac{1}{2}$,+∞) | C. | [2,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
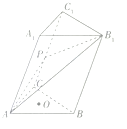 如图所示,在三棱锥ABC-A1B1C1中,底面△ABC为边长为6的等边三角形,点A1在平面ABC内的射影为△ABC的中心.
如图所示,在三棱锥ABC-A1B1C1中,底面△ABC为边长为6的等边三角形,点A1在平面ABC内的射影为△ABC的中心.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | B. | $\frac{y^2}{16}-\frac{x^2}{9}=1$ | C. | $\frac{y^2}{36}-\frac{x^2}{64}=1$ | D. | $\frac{x^2}{64}-\frac{y^2}{36}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
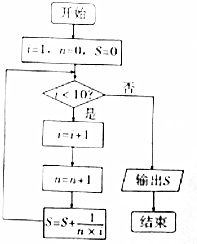
| A. | $\frac{7}{8}$ | B. | $\frac{8}{9}$ | C. | $\frac{9}{10}$ | D. | $\frac{10}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com