
分析 ①取BD的中点E,则AE⊥BD,CE⊥BD.根据线面垂直的判定及性质可判断,
②求出AB与平面BCD所成的角可判断
③求出三角形ABC各边的长度进行比较即可判断,
④根据EA=EB=EC=ED=$\sqrt{2}$得到球的半径,进行判断即可.
解答 解:①取BD中点E,连结AE,CE,则AE⊥BD,CE⊥BD,∴BD⊥平面ACE,∴AC⊥BD.故①正确.
②∠ABD为AB与面BCD所成的角为45°,故②错误.
③∵折叠前正方形的边长为2,∴BD=2$\sqrt{2}$,∴AE=CE=$\sqrt{2}$.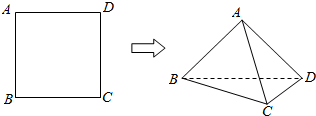
∵平面ABD⊥平面BCD,∴AE⊥平面BCD,∴AE⊥CE,∴AC=$\sqrt{A{E}^{2}+C{E}^{2}}$=2.
∴△ABC是等边三角形,故③正确.
④∵折叠前正方形的边长为2,则BD=2$\sqrt{2}$,
∴EA=EB=EC=ED=$\sqrt{2}$.
若A、B、C、D四点在同一个球面上,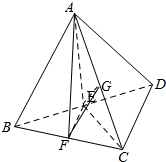
则球的半径r=$\sqrt{2}$,
则该球的表面积S=4π•($\sqrt{2}$)2=8π,故④正确,
故答案为:①③④
点评 本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,难度不大.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 9 | D. | 22 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
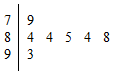 如图,是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
如图,是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A. | 84,4.84 | B. | 84,1.6 | C. | 85,2.4 | D. | 85,1.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com