练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．抛掷一枚骰子一次，出现“点数不小于5”的概率为$\frac{1}{3}$．

    分析 根据古典槪型的概率公式即可得到结论．

    解答 解：将一枚质地均匀的骰子抛掷一次共有6个结果，
    则出现“出现“点数不小于5”，包含2个结果，
    则出现“出现“点数不小于5”的概率P=$\frac{2}{6}$=$\frac{1}{3}$，
    故答案为：$\frac{1}{3}$

    点评 本题主要考查概率的计算，利用古典概率的公式是解决本题的关键，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    10．椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F1，F2，点P在椭圆上，如果PF1的中点在y轴上，且|PF1|=$\frac{5}{3}$|PF2|，则椭圆的离心率e为$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．在数列{an}中，若a2n=2a2n-2+1，a16=127，则a2的值为（　　）
    A．-1B．0C．2D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

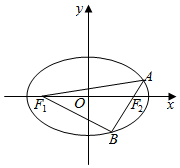    8．已知中心在原点O的椭圆左，右焦点分别为F1，F2，F2（1，0），且椭圆过点（1，$\frac{3}{2}$）．
    （1）求椭圆的方程；
    （2）过F2的直线l与椭圆交于不同的两点A，B，则△F1AB的内切圆的面积是否存在最大值？若存在，求出这个最大值及此时的直线方程；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．设F1、F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点，P是双曲线右支上一点，满足（$\overrightarrow{OP}$+$\overrightarrow{O{F}_{2}}$）•$\overrightarrow{P{F}_{2}}$=0（O为坐标原点），且3|$\overrightarrow{P{F}_{1}}$|=4|$\overrightarrow{P{F}_{2}}$|，则双曲线的离心率为（　　）
    A．2B．$\sqrt{3}$C．$\sqrt{2}$D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．已知数列{an}是公比大于1的等比数列，且a3+a5=20，a4=8，则其前n项和Sn=2n-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．函数f（x）=（2a+1）x+b与g（x）=x2-2（1-a）x+2在（-∞，4]上都是递减的，实数a的取值范围是（　　）
    A．（-∞，-3]B．（-∞，-3）C．[-3，-$\frac{1}{2}$）D．（-3，-$\frac{1}{2}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．如图，一楼高AB为17.5m，某广告公司在楼顶安装一块高BC为2m的广告牌，安装过程中，工作人员利用一个高EF为1.5m的仪器检测安装效果，设AE=xm，该仪器观察到广告牌的视角∠BFC=θ．
    （1）若x=8，求tan∠BFC；
    （2）为确保观察效果，要求视角的正切值即tan∠BFC不小于$\frac{1}{18}$，求x的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．执行如图所示的程序框图，输出的S是下列哪个式子的值（　　）
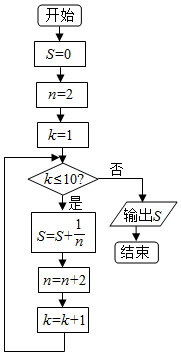
    A．S=1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{10}$B．S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$
    C．S=1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{11}$D．S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{22}$

    查看答案和解析>>

    同步练习册答案