
分析 根据已知直线的斜率,求出渐近线的斜率范围,推出a,b的关系,然后求出离心率的范围.
解答 解:依题意,斜率为$\sqrt{3}$的直线l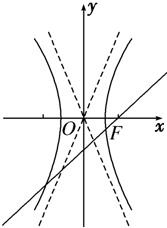 过双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)
过双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)
的右焦点为F且与双曲线的左右两支分别相交,
结合图形分析可知,
双曲线的一条渐近线的斜率$\frac{b}{a}$必大于$\sqrt{3}$,
即$\frac{b}{a}$>$\sqrt{3}$,
因此该双曲线的离心率e=$\frac{c}{a}$=$\sqrt{1+(\frac{b}{a})^{2}}$>$\sqrt{1+3}$=2.
故答案为:(2,+∞).
点评 本题考查直线的斜率,双曲线的应用,考查转化思想,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $-\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2-x+1<0 | B. | ?x∈R,x2-x+1≥0 | C. | ?x∈R,x2-x+1<0 | D. | ?x∈R,x2-x+1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔15000m,速度为1000km/h,飞行员先看到山顶的俯角为15°,经过108s后又看到山顶的俯角为75°,则山顶的海拔高度为6340m.(取$\sqrt{3}$=1.732)
如图,飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔15000m,速度为1000km/h,飞行员先看到山顶的俯角为15°,经过108s后又看到山顶的俯角为75°,则山顶的海拔高度为6340m.(取$\sqrt{3}$=1.732)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin$\frac{x}{2}$ | B. | y=cos$\frac{x}{2}$ | C. | y=cos2x | D. | y=sin2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com