Question

9．如图，飞机的航线和山顶在同一个铅垂平面内，已知飞机的高度为海拔15000m，速度为1000km/h，飞行员先看到山顶的俯角为15°，经过108s后又看到山顶的俯角为75°，则山顶的海拔高度为6340m．（取$\sqrt{3}$=1.732）

Answer 1

分析 先求AB的长，在△ABC中，可求BC的长，进而由于CD⊥AD，所以CD=BCsin∠CBD，故可得山顶的海拔高度．

解答 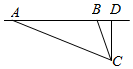解：从山顶C向飞机航向AB作垂线，垂足为D，
则∠CAB=15°，∠CBD=75°，AB=$\frac{1000×1{0}^{3}}{3600}×108$=30000m，
∴∠ACB=60°，
在△ABC中，由正弦定理得$\frac{AB}{sin∠ACB}=\frac{BC}{sin∠CAB}$，
即$\frac{30000}{sin60°}=\frac{BC}{sin15°}$，解得BC=$\frac{30000×\frac{\sqrt{6}-\sqrt{2}}{4}}{\frac{\sqrt{3}}{2}}$=5000（3$\sqrt{2}$-$\sqrt{6}$），
∴CD=BC•sin∠CBD=5000（3$\sqrt{2}$-$\sqrt{6}$）×$\frac{\sqrt{6}+\sqrt{2}}{4}$=5000$\sqrt{3}$，
∴山顶高度为15000-5000$\sqrt{3}$≈6340m．
故答案为：6340．

点评 本题考查了解三角形的应用，正弦定理，属于基础题．