练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f（x）满足f（x+y）=f（x）+f（y），当x＞0时，有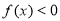，且f（1）=﹣2

    （1）求f（0）及f（﹣1）的值；

    （2）判断函数f（x）的单调性，并利用定义加以证明；

    （3）求解不等式f（2x）﹣f（x2+3x）＜4．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

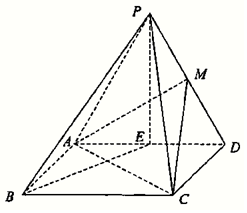    8．如图，在四棱锥P-ABCD中，四边形ABCD是矩形，E，M分别是AD，PD中点，PE⊥BE，PA=PD=AD=2，AB=$\sqrt{2}$．
    （Ⅰ）求证：PB∥平面MAC；
    （Ⅱ）求证：PE⊥平面ABCD；
    （Ⅲ）求证：平面MAC⊥平面PBE．

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年河南省商丘市高一文下学期期末考数学试卷（解析版） 题型：选择题

    函数的图象关于直线对称，则的值为（ ）

    A．1 B． C． D．

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年河南省商丘市高一理下学期期末考数学试卷（解析版） 题型：选择题

    设向量满足则的最大值等于（ ）

    A． B． C． D．

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年河南省商丘市高一理下学期期末考数学试卷（解析版） 题型：选择题

    已知，则 （ ）

    A． B． C． D．

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年河北省保定市高一上学期期中考试数学试卷（解析版） 题型：解答题

    已知全集U＝R．集合A＝{x|－1≤x<3}，B＝{x|x－k≤0}．

    （1）若k＝1，求A∩（∁UB）；

    （2）若A∩B≠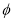，求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．将一块边长为6cm的正方形纸片，先按如图1所示的阴影部分截去四个全等的等腰三角形，然后将剩余部分沿虚线折叠并拼成一个正四棱锥模型（底面是正方形，从顶点向底面作垂线，垂足是底面中心的四棱锥），将该四棱锥如图2放置，若其正视图为正三角形，则其体积为$\frac{8\sqrt{6}}{3}$cm3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．设函数f（x）=$\frac{（x+2）^{2}+sinx}{{x}^{2}+4}$的最大值为M，最小值为m，则M+m=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．某设备的使用年数x与所支出的维修总费用y的统计数据如下表：
    使用年数x（单位：年）23456
    维修费用y（单位：万元）1.54.55.56.57.0
    根据上标可得回归直线方程为$\widehat{y}$=1.3x+$\widehat{a}$，若该设备维修总费用超过12万元，据此模型预测该设备最多可使用9年．

    查看答案和解析>>

    同步练习册答案