
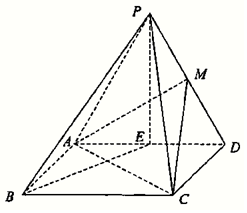
 如图,在四棱锥P-ABCD中,四边形ABCD是矩形,E,M分别是AD,PD中点,PE⊥BE,PA=PD=AD=2,AB=$\sqrt{2}$.
如图,在四棱锥P-ABCD中,四边形ABCD是矩形,E,M分别是AD,PD中点,PE⊥BE,PA=PD=AD=2,AB=$\sqrt{2}$.分析 (Ⅰ)连接BD,交AC于O,连接OE,则OM∥PB,利用线面平行的判定定理证明:PB∥平面MAC;
(Ⅱ)证明PE⊥AD,利用PE⊥BE,BE∩AD=E,证明:PE⊥平面ABCD;
(Ⅲ)证明AC⊥平面PBE,即可证明:平面MAC⊥平面PBE.
解答 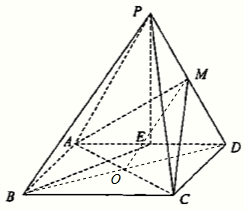 (Ⅰ)连接BD,交AC于O,连接OE,则OM∥PB,
(Ⅰ)连接BD,交AC于O,连接OE,则OM∥PB,
∵PB?平面MAC,OM?平面MAC,
∴PB∥平面MAC;
(Ⅱ)∵PA=PD,E是AD的中点,
∴PE⊥AD,
∵PE⊥BE,BE∩AD=E,
∴PE⊥平面ABCD;
(Ⅲ)∵PE⊥平面ABCD,AC?平面ABCD,
∴AC⊥PE,
∵AD=2,AB=$\sqrt{2}$,四边形ABCD是矩形,E是AD中点,
∴△ABE∽△DAC,
∴∠ABE=∠DAC,
∴AC⊥BE,
∵PE∩BE=E,
∴AC⊥平面PBE,
∵AC?平面MAC,
∴平面MAC⊥平面PBE.
点评 本题考查线面平行、线面垂直的证明,考查面面垂直的证明,考查学生分析解决问题的能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年湖北省仙桃市高一下学期期末考试数学试卷(解析版) 题型:解答题
某中学的高二(1)班男同学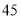 名,女同学
名,女同学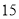 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个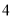 人的课外兴趣小组.
人的课外兴趣小组.
(1)求某同学被抽到的概率及课外兴趣小组中男、女同学的人数;
(2)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出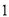 名同学做实验,该同学做完后,再从小组内剩下的同学中选
名同学做实验,该同学做完后,再从小组内剩下的同学中选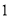 名同学做实验,求选出的两名同学中恰有
名同学做实验,求选出的两名同学中恰有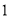 名女同学的概率;
名女同学的概率;
(3)实验结束后,第一次做实验的同学得到的实验数据为 ,第二次做实验的同学得到的实验数据为
,第二次做实验的同学得到的实验数据为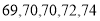 ,请问哪位同学的实验更稳定?并说明理由.
,请问哪位同学的实验更稳定?并说明理由.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河南省商丘市高一文下学期期末考数学试卷(解析版) 题型:解答题
四边形ABCD的内角A与C互补,AB=1,BC=3,CD=DA=2.
(Ⅰ)求C和BD;
(Ⅱ)求四边形ABCD的面积.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北省保定市高一上学期期中考试数学试卷(解析版) 题型:解答题
已知函数f(x)满足f(x+y)=f(x)+f(y),当x>0时,有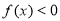 ,且f(1)=﹣2
,且f(1)=﹣2
(1)求f(0)及f(﹣1)的值;
(2)判断函数f(x)的单调性,并利用定义加以证明;
(3)求解不等式f(2x)﹣f(x2+3x)<4.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com