
 将一块边长为6cm的正方形纸片,先按如图1所示的阴影部分截去四个全等的等腰三角形,然后将剩余部分沿虚线折叠并拼成一个正四棱锥模型(底面是正方形,从顶点向底面作垂线,垂足是底面中心的四棱锥),将该四棱锥如图2放置,若其正视图为正三角形,则其体积为$\frac{8\sqrt{6}}{3}$cm3.
将一块边长为6cm的正方形纸片,先按如图1所示的阴影部分截去四个全等的等腰三角形,然后将剩余部分沿虚线折叠并拼成一个正四棱锥模型(底面是正方形,从顶点向底面作垂线,垂足是底面中心的四棱锥),将该四棱锥如图2放置,若其正视图为正三角形,则其体积为$\frac{8\sqrt{6}}{3}$cm3. 分析 根据图形正四棱锥的正视图是正三角形,正视图的底面边长为a,高为$\frac{\sqrt{3}}{2}$a,正四棱锥的斜高为a,运用图1得出$\frac{\sqrt{2}}{2}$×6=a+$\frac{a}{2}$,a=2$\sqrt{2}$,计算出a,代入公式即可.
解答 解: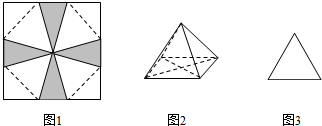
∵正四棱锥的正视图是正三角形,正视图的底面边长为a,高为$\frac{\sqrt{3}}{2}$a,
∴正四棱锥的斜高为a,
∵图1得出:∵将一张边长为6cm的纸片按如图1所示的阴影部分截去四个全等的等腰三角形
∴$\frac{\sqrt{2}}{2}$×6=a+$\frac{a}{2}$,a=2$\sqrt{2}$
∴正四棱锥的体积是$\frac{1}{3}$a2×$\frac{\sqrt{3}}{2}$a=$\frac{8\sqrt{6}}{3}$cm3,
故答案为$\frac{8\sqrt{6}}{3}$.
点评 本题综合考查了空间几何体的性质,展开图与立体图的结合,需要很好的空间思维能力,属于中档题.


科目:高中数学 来源:2015-2016学年河南省商丘市高一理下学期期末考数学试卷(解析版) 题型:解答题
四边形ABCD的内角A与C互补,AB=1,BC=3,CD=DA=2.
(Ⅰ)求C和BD;
(Ⅱ)求四边形ABCD的面积.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北省保定市高一上学期期中考试数学试卷(解析版) 题型:解答题
已知函数f(x)满足f(x+y)=f(x)+f(y),当x>0时,有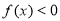 ,且f(1)=﹣2
,且f(1)=﹣2
(1)求f(0)及f(﹣1)的值;
(2)判断函数f(x)的单调性,并利用定义加以证明;
(3)求解不等式f(2x)﹣f(x2+3x)<4.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com