
分析 由条件可得$\frac{2}{2y}$+$\frac{8}{x-2y}$=10-$\frac{1}{2}$x,即有[2y+(x-2y)]($\frac{2}{2y}$+$\frac{8}{x-2y}$)=(10-$\frac{1}{2}$x)x,将等式左边展开,运用基本不等式可得x的二次不等式,解不等式可得x的最大值.
解答 解:x>2y>0,且满足$\frac{x}{2}+\frac{1}{y}+\frac{8}{x-2y}$=10,
可得$\frac{2}{2y}$+$\frac{8}{x-2y}$=10-$\frac{1}{2}$x,
即有[2y+(x-2y)]($\frac{2}{2y}$+$\frac{8}{x-2y}$)=(10-$\frac{1}{2}$x)x,
可得10+$\frac{2(x-2y)}{2y}$+$\frac{16y}{x-2y}$=(10-$\frac{1}{2}$x)x≥10+2$\sqrt{\frac{2(x-2y)}{2y}•\frac{16y}{x-2y}}$=18,
当且仅当x-2y=4y,即x=6y,取得等号.
即有x2-20x+36≤0,
解得2≤x≤18.
可得x的最大值18.
故答案为:18.
点评 本题考查最值的求法,注意运用变形和基本不等式,考查转化思想,转化为x的二次不等式,考查运算能力,属于中档题.


科目:高中数学 来源:2015-2016学年河北省保定市高一上学期期中考试数学试卷(解析版) 题型:解答题
已知全集U=R.集合A={x|-1≤x<3},B={x|x-k≤0}.
(1)若k=1,求A∩(∁UB);
(2)若A∩B≠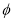 ,求k的取值范围.
,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 将一块边长为6cm的正方形纸片,先按如图1所示的阴影部分截去四个全等的等腰三角形,然后将剩余部分沿虚线折叠并拼成一个正四棱锥模型(底面是正方形,从顶点向底面作垂线,垂足是底面中心的四棱锥),将该四棱锥如图2放置,若其正视图为正三角形,则其体积为$\frac{8\sqrt{6}}{3}$cm3.
将一块边长为6cm的正方形纸片,先按如图1所示的阴影部分截去四个全等的等腰三角形,然后将剩余部分沿虚线折叠并拼成一个正四棱锥模型(底面是正方形,从顶点向底面作垂线,垂足是底面中心的四棱锥),将该四棱锥如图2放置,若其正视图为正三角形,则其体积为$\frac{8\sqrt{6}}{3}$cm3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 5 | C. | 10 | D. | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com