
分析 化f(x)为1+$\frac{4x+sinx}{{x}^{2}+4}$,由g(x)=$\frac{4x+sinx}{{x}^{2}+4}$,定义域为R,判断g(x)的奇偶性,由图象性质可得g(x)的最值之和为0,进而得到所求和.
解答 解:函数f(x)=$\frac{(x+2)^{2}+sinx}{{x}^{2}+4}$
=$\frac{{x}^{2}+4+4x+sinx}{{x}^{2}+4}$=1+$\frac{4x+sinx}{{x}^{2}+4}$,
由g(x)=$\frac{4x+sinx}{{x}^{2}+4}$,定义域为R,
可得g(-x)+g(x)=$\frac{-4x-sinx}{{x}^{2}+4}$+$\frac{4x+sinx}{{x}^{2}+4}$=0,
可得g(x)为奇函数,
由奇函数的图象关于原点对称,
可得g(x)的最大值a与最小值b的和为0,
则M+m=a+1+b+1=(a+b)+2=2.
故答案为:2.
点评 本题考查函数的最值的求法,注意运用转化法,由奇函数的性质:最值之和为0,考查运算能力,属于中档题.


科目:高中数学 来源:2015-2016学年河南省商丘市高一文下学期期末考数学试卷(解析版) 题型:解答题
四边形ABCD的内角A与C互补,AB=1,BC=3,CD=DA=2.
(Ⅰ)求C和BD;
(Ⅱ)求四边形ABCD的面积.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北省保定市高一上学期期中考试数学试卷(解析版) 题型:解答题
已知函数f(x)满足f(x+y)=f(x)+f(y),当x>0时,有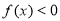 ,且f(1)=﹣2
,且f(1)=﹣2
(1)求f(0)及f(﹣1)的值;
(2)判断函数f(x)的单调性,并利用定义加以证明;
(3)求解不等式f(2x)﹣f(x2+3x)<4.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 4$\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com