
| 使用年数x(单位:年) | 2 | 3 | 4 | 5 | 6 |
| 维修费用y(单位:万元) | 1.5 | 4.5 | 5.5 | 6.5 | 7.0 |
分析 计算$\overline{x}$、$\overline{y}$,根据回归直线方程过样本中心点求出$\widehat{a}$的值,写出回归直线方程,
利用回归方程求$\widehat{y}$≥12时x的取值即可.
解答 解:计算$\overline{x}$=$\frac{1}{5}$×(2+3+4+5+6)=4,
$\overline{y}$=$\frac{1}{5}$×(1.5+4.5+5.5+6.5+7.0)=5,
又回归直线方程$\widehat{y}$=1.3x+$\widehat{a}$过样本中心点,
∴$\widehat{a}$=$\overline{y}$-1.3$\overline{x}$=5-1.3×4=-0.2,
∴回归直线方程为$\widehat{y}$=1.3x-0.2;
令$\widehat{y}$=1.3x-0.2≥12,
解得x≥9.4≈9,
∴据此模型预测该设备最多可使用9年.
故答案为:9.
点评 本题考查了样本中心点满足回归直线的方程的应用问题,是基础题目.


科目:高中数学 来源:2015-2016学年河北省保定市高一上学期期中考试数学试卷(解析版) 题型:解答题
已知函数f(x)满足f(x+y)=f(x)+f(y),当x>0时,有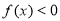 ,且f(1)=﹣2
,且f(1)=﹣2
(1)求f(0)及f(﹣1)的值;
(2)判断函数f(x)的单调性,并利用定义加以证明;
(3)求解不等式f(2x)﹣f(x2+3x)<4.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北省保定市高一上学期期中考试数学试卷(解析版) 题型:选择题
若函数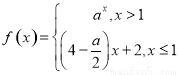 是R上的单调递增函数,则实数a的取值范围为( )
是R上的单调递增函数,则实数a的取值范围为( )
A.(1,+∞) B.(1,8) C.(4,8) D.[4,8)
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 4$\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com