
| A. | g(x)是奇函数 | B. | g(x)关于直线x=-$\frac{π}{4}$对称 | ||
| C. | g(x)在[$\frac{π}{4}$,$\frac{π}{2}$]上是增函数 | D. | 当x∈[$\frac{π}{6}$,$\frac{2π}{3}$]时,g(x)的值域是[2,1] |
分析 将函数化简,图象与x轴交点的横坐标依次构成一个公差为$\frac{π}{2}$的等差数列,可知周期为π,由周期求出ω,向左平移$\frac{π}{6}$个单位可得g(x)的解析式,再利用三角函数图象及性质,可得结论.
解答 解:f(x)=$\sqrt{3}$sin?x+cosωx(ω>0),
化简得:f(x)=2sin(?x+$\frac{π}{6}$),
∵图象与x轴交点的横坐标依次构成一个公差为$\frac{π}{2}$的等差数列,可知周期为π
∴T=π=$\frac{2π}{ω}$,解得ω=2.
那么:f(x)=2sin(2x+$\frac{π}{6}$),图象沿x轴向左平移$\frac{π}{6}$个单位,得:2sin[2(x+$\frac{π}{6}$)+$\frac{π}{6}$]=2cos2x.
∴g(x)=2cos2x,故g(x)是偶函数,在区间[0,$\frac{π}{2}$]单调减函数.所以A,C不对.
对称轴方程为x=$\frac{1}{2}kπ$(k=Z),检验B不对.
当x∈[$\frac{π}{6}$,$\frac{2π}{3}$]时,那么2x∈[$\frac{π}{3}$,$\frac{4π}{3}$],g(x)的最大值为1,最小值为-2,故值域为[-2,1].D正确.
故选:D.
点评 本题考查了三角函数的辅助角公式的化简和图象的平移,三角函数的性质的运用能力.属于中档题.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:选择题
| A. | 若$\overrightarrow a•\overrightarrow b=\overrightarrow a•\overrightarrow c$,则$\overrightarrow b=\overrightarrow c$ | B. | 若$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a-\overrightarrow b}|$,则$\overrightarrow a•\overrightarrow b=0$ | ||
| C. | 若$\overrightarrow a∥\overrightarrow b,\overrightarrow b∥\overrightarrow c$,则$\overrightarrow a∥\overrightarrow c$ | D. | 若$\overrightarrow a$与$\overrightarrow b$是单位向量,则$\overrightarrow a•\overrightarrow b=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
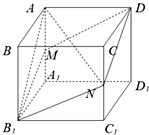 已知正方体ABCD-A1B1C1D1的棱长为a,M,N分别是棱AA1,CC1的中点,
已知正方体ABCD-A1B1C1D1的棱长为a,M,N分别是棱AA1,CC1的中点,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (-∞,-2) | C. | (-2,0) | D. | (-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com