
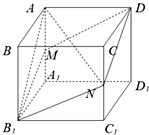
 已知正方体ABCD-A1B1C1D1的棱长为a,M,N分别是棱AA1,CC1的中点,
已知正方体ABCD-A1B1C1D1的棱长为a,M,N分别是棱AA1,CC1的中点,分析 (Ⅰ)内切球的直径是AB,外接球的直径是AC1,由此能求出内切球与外接球半径之比.
(Ⅱ)连结MN,则${V_{A-M{B_1}ND}}={V_{A-M{B_1}N}}+{V_{A-MND}}$${V_{A-M{B_1}N}}={V_{N-AM{B_1}}}=\frac{1}{3}•a•{S_{△AM{B_1}}}$,由此能求出四棱锥A-MB1ND的体积.
解答 解:(Ⅰ)由题意,内切球的直径是AB,外接球的直径是AC1,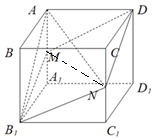
∴内切球半径$r=\frac{1}{2}a$,外接球半径$R=\frac{{\sqrt{3}}}{2}a$,
∴内切球与外接球半径之比为$1:\sqrt{3}$.
(Ⅱ)连结MN,
则${V_{A-M{B_1}ND}}={V_{A-M{B_1}N}}+{V_{A-MND}}$${V_{A-M{B_1}N}}={V_{N-AM{B_1}}}=\frac{1}{3}•a•{S_{△AM{B_1}}}$,
∵${S_{△AM{B_1}}}=\frac{1}{2}•AM•{B_1}{A_1}=\frac{1}{2}•\frac{1}{2}a•a=\frac{1}{4}{a^2}$,
∴${V_{A-M{B_1}N}}=\frac{1}{3}•a•\frac{1}{4}{a^2}=\frac{1}{12}{a^3}$,${V_{A-MND.}}={V_{N-AMD}}=\frac{1}{3}•a•{S_{△AM{D_1}}}$,
∵${S_{△AM{B_1}}}=\frac{1}{2}•AM•AD=\frac{1}{2}•\frac{1}{2}a•a=\frac{1}{4}{a^2}$,
∴${V_{A-MND}}=\frac{1}{3}•a•\frac{1}{4}{a^2}=\frac{1}{12}{a^3}$,
综上,四棱锥A-MB1ND的体积${V_{A-M{B_1}ND}}={V_{A-M{B_1}N}}+{V_{A-MND}}=\frac{1}{6}{a^3}$.
点评 本题考查正方体的内切球与外接球的半径之比,考查四棱锥的体积的求法,是中档题,解题时要认真审题,注意正方体的性质的合理运用.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
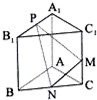 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=l,AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足$\overrightarrow{{A_1}P}$=λ$\overrightarrow{{A_1}{B_1}}$.
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=l,AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足$\overrightarrow{{A_1}P}$=λ$\overrightarrow{{A_1}{B_1}}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②④ | B. | ①④ | C. | ③④ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | g(x)是奇函数 | B. | g(x)关于直线x=-$\frac{π}{4}$对称 | ||
| C. | g(x)在[$\frac{π}{4}$,$\frac{π}{2}$]上是增函数 | D. | 当x∈[$\frac{π}{6}$,$\frac{2π}{3}$]时,g(x)的值域是[2,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,2) | B. | (0,1) | C. | (-1,1) | D. | (-1,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com