
| A. | ①②④ | B. | ①④ | C. | ③④ | D. | ①②③ |
分析 ①利用余弦的倍角公式进行化简,结合三角函数的周期公式进行求解即可,
②根据等比数列的性质进行求解,
③根据函数定义域的性质建立不等式关系进行求解,
④根据向量相等以及向量数量积的性质进行判断即可.
解答 解:①函数f(x)=sin2x-cos2x=-cos2x,则函数的周期T=$\frac{2π}{2}$=π;故①正确,
②在等比数列{an}中,若a1=1,a5=4,则a32=a1a5=4,则a3=±2;故②正确,
③设函数f(x)=$\frac{x+m}{x+1}$(m≠1),则函数的定义域为{x|x≠-1},
若f($\frac{2t-1}{t}$)有意义,则$\left\{\begin{array}{l}{\frac{2t-1}{t}≠-1}\\{t≠0}\end{array}\right.$,即$\left\{\begin{array}{l}{t≠\frac{1}{3}}\\{t≠0}\end{array}\right.$,则t≠0且t$≠\frac{1}{3}$;故③错误,
④平面四边形ABCD中,$\overrightarrow{AB}$+$\overrightarrow{CD}$=$\overrightarrow{0}$,
则$\overrightarrow{AB}$=-$\overrightarrow{CD}$=$\overrightarrow{DC}$,
则四边形ABCD为平行四边形,
∵($\overrightarrow{AB}$-$\overrightarrow{AD}$)•$\overrightarrow{AC}$=0,
∴$\overrightarrow{DB}$•$\overrightarrow{AC}$=0,
则四边形ABCD的对角线垂直,
则四边形ABCD是菱形.故④正确,
故选:A.
点评 本题主要考查命题的真假判断,涉及知识点较多,综合性较多,考查学生的运算和推理能力.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | a>1 | B. | a>$\frac{3}{2}$ | C. | a>2 | D. | a>3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
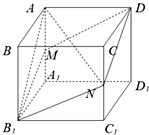 已知正方体ABCD-A1B1C1D1的棱长为a,M,N分别是棱AA1,CC1的中点,
已知正方体ABCD-A1B1C1D1的棱长为a,M,N分别是棱AA1,CC1的中点,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
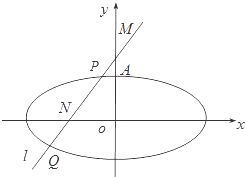 已知F1,F2,A分别为椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左右焦点及上顶点△AF1F2的面积为4$\sqrt{3}$且椭圆的离心率等于$\frac{{\sqrt{3}}}{2}$,过点M(0,4)的直线l与椭圆相交于不同的两点P、Q,点N在线段PQ上.
已知F1,F2,A分别为椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左右焦点及上顶点△AF1F2的面积为4$\sqrt{3}$且椭圆的离心率等于$\frac{{\sqrt{3}}}{2}$,过点M(0,4)的直线l与椭圆相交于不同的两点P、Q,点N在线段PQ上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com