
分析 由题意,an=$\frac{1}{(\sqrt{n-1}+\sqrt{n})(\sqrt{n}+\sqrt{n+1})(\sqrt{n-1}+\sqrt{n+1})}$=$\frac{1}{2}$•($\frac{1}{\sqrt{n-1}+\sqrt{n}}$-$\frac{1}{\sqrt{n}+\sqrt{n+1}}$)=$\frac{1}{2}$[($\sqrt{n}$-$\sqrt{n-1}$)-($\sqrt{n+1}$-$\sqrt{n}$)],利用叠加法即可得出结论.
解答 解:由题意,an=$\frac{1}{(\sqrt{n-1}+\sqrt{n})(\sqrt{n}+\sqrt{n+1})(\sqrt{n-1}+\sqrt{n+1})}$=$\frac{1}{2}$•($\frac{1}{\sqrt{n-1}+\sqrt{n}}$-$\frac{1}{\sqrt{n}+\sqrt{n+1}}$)
=$\frac{1}{2}$[($\sqrt{n}$-$\sqrt{n-1}$)-($\sqrt{n+1}$-$\sqrt{n}$)],
∴S2009=$\frac{1}{2}$[(1-0+$\sqrt{2}$-1+…+$\sqrt{2009}$-$\sqrt{2008}$)-($\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+…+$\sqrt{2010}$-$\sqrt{2009}$)]
=$\frac{1}{2}$($\sqrt{2009}$-$\sqrt{2010}$+1).
故答案为$\frac{1}{2}$($\sqrt{2009}$-$\sqrt{2010}$+1).
点评 本题考查数列的求和,考查叠加法的运用,正确化简通项是关键.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
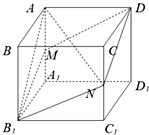 已知正方体ABCD-A1B1C1D1的棱长为a,M,N分别是棱AA1,CC1的中点,
已知正方体ABCD-A1B1C1D1的棱长为a,M,N分别是棱AA1,CC1的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (-∞,-2) | C. | (-2,0) | D. | (-2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com