
分析 (1)由题意可设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).由双曲线$\frac{x^2}{3}-{y^2}=1$,可得焦点(±2,0).可得a=2,又$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,a2=b2+c2,联立解出即可得出.
(2)由(1)可得:F1$(-\sqrt{3},0)$,F2$(\sqrt{3},0)$.设P(x0,y0),(x0,y0>0),由$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=-$\frac{5}{4}$,可得${x}_{0}^{2}$+${y}_{0}^{2}$-3=$-\frac{5}{4}$,又$\frac{{x}_{0}^{2}}{4}$+${y}_{0}^{2}$=1,联立解出即可得出.
(3)设A(x1,y1),B(x2,y2),直线l的方程为:y=kx+2,与椭圆方程联立可得:(1+4k2)x2+16kx+12=0,△>0,解得:k2$>\frac{3}{4}$.由∠AOB为锐角(其中O为原点),可得$\overrightarrow{OA}•\overrightarrow{OB}$>0,且A,O,B三点不共线.利用数量积运算性质、一元二次方程的根与系数的关系即可得出.
解答 解:(1)由题意可设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).
由双曲线$\frac{x^2}{3}-{y^2}=1$,可得焦点(±2,0).
∴a=2,又$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,a2=b2+c2,
联立解得:a=2,c=$\sqrt{3}$,b=1.
∴椭圆C的方程为:$\frac{{x}^{2}}{4}$+y2=1.
(2)由(1)可得:F1$(-\sqrt{3},0)$,F2$(\sqrt{3},0)$.
设P(x0,y0),(x0,y0>0),
∵$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=-$\frac{5}{4}$,∴${x}_{0}^{2}$+${y}_{0}^{2}$-3=$-\frac{5}{4}$,
又$\frac{{x}_{0}^{2}}{4}$+${y}_{0}^{2}$=1,联立解得:x0=1,y0=$\frac{\sqrt{3}}{2}$.
∴点P$(1,\frac{\sqrt{3}}{2})$.
(3)设A(x1,y1),B(x2,y2),直线l的方程为:y=kx+2,
联立$\left\{\begin{array}{l}{y=kx+2}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$,化为:(1+4k2)x2+16kx+12=0,
△=256k2-48(1+4k2)>0,解得:k2$>\frac{3}{4}$.
∴x1+x2=-$\frac{16k}{1+4{k}^{2}}$,x1x2=$\frac{12}{1+4{k}^{2}}$.
∵∠AOB为锐角(其中O为原点),
∴$\overrightarrow{OA}•\overrightarrow{OB}$>0,且A,O,B三点不共线.
由$\overrightarrow{OA}•\overrightarrow{OB}$>0,可得:x1x2+y1y2=x1x2+(kx1+2)(kx2+2)>0,
可得:(1+k2)x1x2+2k(x1+x2)+4>0,
∴(1+k2)×$\frac{12}{1+4{k}^{2}}$-2k×$\frac{16k}{1+4{k}^{2}}$+4>0,
化为:k2<3,
又k2$>\frac{3}{4}$,∴$-\sqrt{3}<k<-\frac{\sqrt{3}}{2}$,或$\frac{\sqrt{3}}{2}$<k$<\sqrt{3}$.
∵A,O,B三点不共线时,斜率不存在,
∴直线l斜率k的取值范围是:$(-\sqrt{3},-\frac{\sqrt{3}}{2})$∪$(\frac{\sqrt{3}}{2},\sqrt{3})$.
点评 本题考查了椭圆的定义标准方程及其性质、数量积运算性质、一元二次方程的根与系数的关系、不等式的解法、数量积运算性质,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
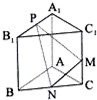 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=l,AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足$\overrightarrow{{A_1}P}$=λ$\overrightarrow{{A_1}{B_1}}$.
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=l,AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足$\overrightarrow{{A_1}P}$=λ$\overrightarrow{{A_1}{B_1}}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com