Question

已知x=是的一个极值点
(Ⅰ)求的值；
(Ⅱ)求函数的单调增区间；
(Ⅲ)设，试问过点（2，5）可作多少条曲线y=g(x)的切线？为什么？

Answer 1

(1) b=" -1" (2) 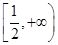 (3) 过点（2，5）可作2条曲线y=g(x)的切线

解析试题分析：解：(1) 因x=－1是的一个极值点
∴
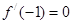
即 2+b-1=0
∴b= -1经检验，适合题意，所以b= -1． （7分）
(2)  
∴>0
∴ >0
∴x>∴函数的单调增区间为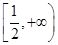 （14分）
（3）=2x+lnx
设过点（2，5）与曲线g (x)的切线的切点坐标为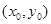
∴
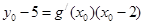
即   ∴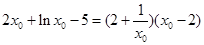
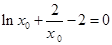
令h(x)=
∴==0
∴
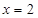
∴h(x)在（0，2）上单调递减，在（2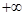，）上单调递增
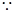又，h(2)=ln2-1<0，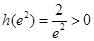
∴h(x)与x轴有两个交点
∴过点（2，5）可作2条曲线y=g(x)的切线. ……（16分）
考点：导数的运用
点评：本试题主要是考查了导数的几何意义，以及函数极值和最值的运用，属于基础题。