
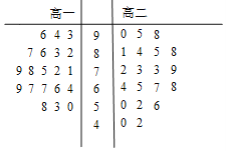
【题目】某学校为了解学生的体质健康状况,对高一、高二两个年级的学生进行了体质测试.现从两个年级学生中各随机选取20人,将他们的测试数据,用茎叶图表示如图:《国家学生体质健康标准》的等级标准如表.规定:测试数据≥60,体质健康为合格.
等级 | 优秀 | 良好 | 及格 | 不及格 |
测试数据 |
|
|
|
|
(Ⅰ)从该校高二年级学生中随机选取一名学生,试估计这名学生体质健康合格的概率;
(Ⅱ)从两个年级等级为优秀的样本中各随机选取一名学生,求选取的两名学生的测试数据平均数大于95的概率;
(Ⅲ)设该校高一学生测试数据的平均数和方差分别为![]() ,高二学生测试数据的平均数和方差分别为
,高二学生测试数据的平均数和方差分别为![]() ,试估计
,试估计![]() 、
、![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
【答案】(I)![]() ;(II)
;(II)![]() ;(III)
;(III)![]()
【解析】
(Ⅰ)由茎叶图可知高二年级学生样本中合格的学生数为15,即可计算出从该校高二年级学生中随机选取一名学生体质健康合格的概率;
(Ⅱ)由茎叶图可知高一年级、高二年级等级为优的学生各有三个,用列举法写出选取的两名学生构成的基本事件,即可计算出选取的两名学生的测试数据平均数大于95的概率;
(Ⅲ)根据茎叶图的分布情况即可得到![]() 、
、![]() 的大小。
的大小。
(I)高二年级学生样本中合格的学生数为:![]() ,
,
样本中学生体质健康合格的频率为![]() .
.
所以从该校高二年级学生中随机选取一名学生,估计这名学生体质健康合格的概率为![]() .
.
(II) 设等级为优秀的样本中高一年级测试数据是93,94,96的学生分别为![]() ,
,
高二年级测试数据是90,95,98的学生分别为![]() .
.
选取的两名学生构成的基本事件空间为:
![]() ,总数为9,
,总数为9,
选取的测试数据平均数大于95的两名学生构成的基本事件空间为![]() ,总数为4,
,总数为4,
所以从两个年级等级为优秀的样本中各随机选取一名学生,
选取的两名学生的测试数据平均数大于95的概率为![]() .
.
(III)![]() .
.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
【题目】某企业为确定下一年投入某种产品的研发费用,需了解年研发费用![]() (单位:千万元)对年销售量
(单位:千万元)对年销售量![]() (单位:千万件)的影响,统计了近
(单位:千万件)的影响,统计了近![]() 年投入的年研发费用
年投入的年研发费用![]() 与年销售量
与年销售量![]() 的数据,得到散点图如图所示:
的数据,得到散点图如图所示:
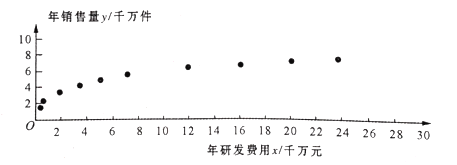
(Ⅰ)利用散点图判断,![]() 和
和![]() (其中
(其中![]() ,
,![]() 为大于
为大于![]() 的常数)哪一个更适合作为年研发费用
的常数)哪一个更适合作为年研发费用![]() 和年销售量
和年销售量![]() 的回归方程类型(只要给出判断即可,不必说明理由);
的回归方程类型(只要给出判断即可,不必说明理由);
(Ⅱ)对数据作出如下处理:令![]() ,
,![]() ,得到相关统计量的值如下表:
,得到相关统计量的值如下表:

根据(Ⅰ)的判断结果及表中数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅲ)已知企业年利润![]() (单位:千万元)与
(单位:千万元)与![]() ,
,![]() 的关系为
的关系为![]() (其中
(其中![]() ),根据(Ⅱ)的结果,要使得该企业下一年的年利润最大,预计下一年应投入多少研发费用?
),根据(Ⅱ)的结果,要使得该企业下一年的年利润最大,预计下一年应投入多少研发费用?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为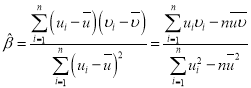 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年1月6日北京时间上午11时30分,朝鲜中央电视台宣布“成功进行了氢弹试验”,再次震动世界,此事件也引起了我国公民热议,其中丹东市(丹东市和朝鲜隔江)某QQ聊天群有300名网友,乌鲁木齐市某微信群有200名网友,为了解不同地区我国公民对“氢弹试验”事件的关注程度,现采用分层抽样的方法,从中抽取了100名网友,先分别统计了他们在某时段发表的信息条数,再将两地网友发表的信息条数分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,分别加以统计,得到如图所示的频率分布直方图.
,分别加以统计,得到如图所示的频率分布直方图.
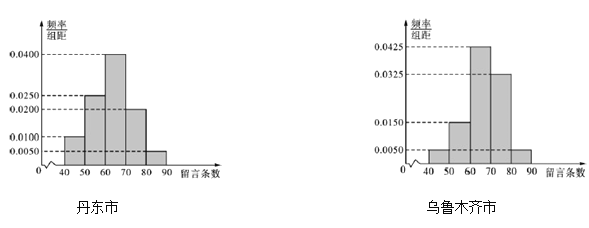
(1)求丹东市网友的平均留言条数(保留整数);
(2)为了进一步开展调查,从样本中留言条数超过80条的网友中随机抽取2人,求至少抽到一名乌鲁木齐市网友的概率;
(3)规定“留言条数”不少于70条为“强烈关注”.
①请你根据已知条件完成下列2×2的列联表:
强烈关注 | 非强烈关注 | 合计 | |
丹东市 | |||
乌鲁木齐市 | |||
合计 |
②判断是否有90%的把握认为“强烈关注”与网友所在的地区有关?
附:临界值表及参考公式:
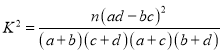 ,
,![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点.
的左、右焦点.
(1)若![]() 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求![]() 的最大值和最小值;
的最大值和最小值;
(2)设过定点![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,且
,且![]() 为锐角(其中
为锐角(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PCD⊥平面ABCD,AB=2,BC=1,![]() ,E为PB中点.
,E为PB中点.
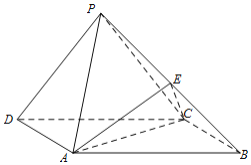
(Ⅰ)求证:PD∥平面ACE;
(Ⅱ)求证:PD⊥平面PBC;
(Ⅲ)求三棱锥E-ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() (如图1)的平面展开图(如图2)中,四边形
(如图1)的平面展开图(如图2)中,四边形![]() 为边长为
为边长为![]() 的正方形,△ABE和△BCF均为正三角形,在三棱锥
的正方形,△ABE和△BCF均为正三角形,在三棱锥![]() 中:
中:
(I)证明:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)若点![]() 在棱
在棱![]() 上,满足
上,满足![]() ,
, ![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() ,求
,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种类型的题目有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 5个选项,其中有3个正确选项,满分5分.赋分标准为“选对1个得2分,选对2个得4分,选对3个得5分,每选错1个扣3分,最低得分为0分”在某校的一次考试中出现了一道这种类型的题目,已知此题的正确答案为
5个选项,其中有3个正确选项,满分5分.赋分标准为“选对1个得2分,选对2个得4分,选对3个得5分,每选错1个扣3分,最低得分为0分”在某校的一次考试中出现了一道这种类型的题目,已知此题的正确答案为![]() ,假定考生作答的答案中的选项个数不超过3个.
,假定考生作答的答案中的选项个数不超过3个.
(1)若甲同学无法判断所有选项,他决定在这5个选项中任选3个作为答案,求甲同学获得0分的概率;
(2)若乙同学只能判断选项![]() 是正确的,现在他有两种选择:一种是将AD作为答案,另一种是在
是正确的,现在他有两种选择:一种是将AD作为答案,另一种是在![]() 这3个选项中任选一个与
这3个选项中任选一个与![]() 组成一个含有3个选项的答案,则乙同学的最佳选择是哪一种,请说明理由.
组成一个含有3个选项的答案,则乙同学的最佳选择是哪一种,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com