
| 分组 | 频数 | 频率 | 频率/组距 |
| [27,32) | 3 | 0.06 | 0.012 |
| [32,37) | 3 | 0.06 | 0.012 |
| [37,42) | 9 | 0.18 | 0.036 |
| [42,47) | 16 | 0.32 | 0.064 |
| [47,52) | 7 | 0.14 | 0.028 |
| [52,57) | 5 | 0.10 | 0.020 |
| [57,62) | 4 | 0.08 | 0.016 |
| [62,67) | 3 | 0.06 | 0.012 |
分析 (1)根据题意,填写频率分布表即可;
(2)根据频率分布表,画出样本频率分布直方图;
(3)计算样本中体重在37-57kg的频率,估计总体中对应的学生数.
解答 解:(1)根据题意,填写频率分布表,如下;(共(4分),每错一个数据扣一分,扣完为止)
| 分组 | 频数 | 频率 | 频率/组距 |
| [27,32) | 3 | 0.06 | 0.012 |
| [32,37) | 3 | 0.06 | 0.012 |
| [37,42) | 9 | 0.18 | 0.036 |
| [42,47) | 16 | 0.32 | 0.064 |
| [47,52) | 7 | 0.14 | 0.028 |
| [52,57) | 5 | 0.10 | 0.020 |
| [57,62) | 4 | 0.08 | 0.016 |
| [62,67) | 3 | 0.06 | 0.012 |
| 总计 | 50 | 1.00 | 0.200 |
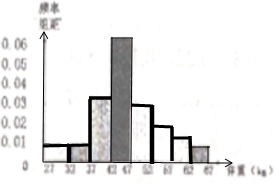
点评 本题考查了频率分布直方图的应用问题,也考查了用样本估计总体的应用问题,是基础题目.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
| 2 | 3 | 4 | 5 | 6 | 7 | … |
| 3 | 5 | 7 | 9 | 11 | 13 | … |
| 4 | 7 | 10 | 13 | 16 | 19 | … |
| 5 | 9 | 13 | 17 | 21 | 25 | … |
| 6 | 11 | 16 | 21 | 26 | 31 | … |
| 7 | 13 | 19 | 25 | 31 | 37 | … |
| … | … | … | … | … | … | … |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com