
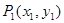 ,
,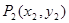 ,…,
,…, ,…是曲线
,…是曲线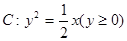 上的点,
上的点,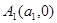 ,
, ,…,
,…, ,…是
,…是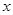 轴正半轴上的点,且
轴正半轴上的点,且 ,
,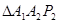 ,…,
,…, ,… 均为斜边在
,… 均为斜边在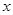 轴上的等腰直角三角形(
轴上的等腰直角三角形( 为坐标原点).
为坐标原点). 、
、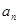 和
和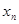 之间的等量关系,以及
之间的等量关系,以及 、
、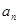 和
和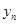 之间的等量关系;
之间的等量关系; (
(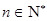 );
);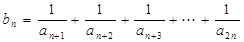 ,对所有
,对所有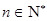 ,
,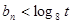 恒成立,求实数
恒成立,求实数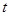 的取值范围.
的取值范围.
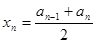 ,
,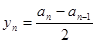 (2)
(2)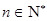 ,
, (3)
(3)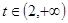
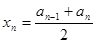 ,
,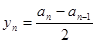 得到
得到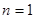 时,可求得
时,可求得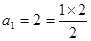 ,命题成立;②假设当
,命题成立;②假设当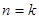 时,命题成立,即有
时,命题成立,即有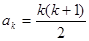 则当
则当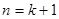 时,由归纳假设及
时,由归纳假设及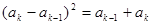 ,
,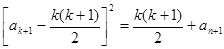
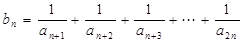
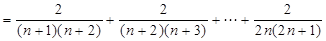
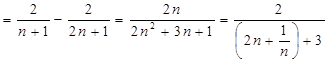 .………………………2分
.………………………2分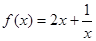 在区间
在区间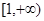 上单调递增,所以当
上单调递增,所以当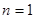 时,
时,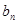 最大为
最大为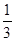 ,即
,即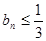
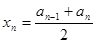 ,
,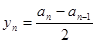 ,………………4分
,………………4分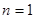 时,可求得
时,可求得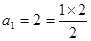 ,命题成立; ……………2分
,命题成立; ……………2分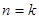 时,命题成立,即有
时,命题成立,即有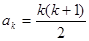 ,……………………1分
,……………………1分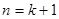 时,由归纳假设及
时,由归纳假设及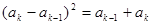 ,
,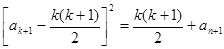 .
.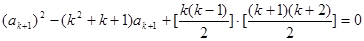
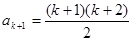 (
(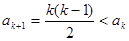 不合题意,舍去)
不合题意,舍去)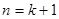 时,命题成立. …………………………………………4分
时,命题成立. …………………………………………4分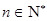 ,
, . ……………………………1分
. ……………………………1分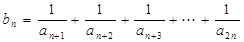
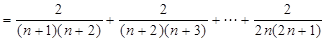
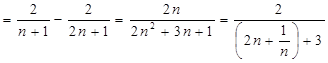 .………………………2分
.………………………2分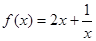 在区间
在区间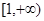 上单调递增,所以当
上单调递增,所以当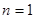 时,
时,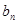 最大为
最大为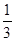 ,即
,即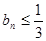 .……………2分
.……………2分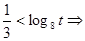
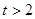 . 所以,
. 所以,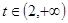


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com