
分析 (Ⅰ)由已知直接求出a2,a3的值,并由累加法求出{an}的通项公式;
(Ⅱ)把数列通项公式代入bn=$\frac{1}{{a}_{n+1}}$+$\frac{1}{{a}_{n+2}}$+$\frac{1}{{a}_{n+3}}$+…+$\frac{1}{{a}_{2n+1}}$,利用裂项相消法化简,求出最大值,可得bn≤m恒成立时实数m的取值范围.
解答 解:(Ⅰ)∵a1=2,an-an-1=2n,∴a2=6,a3=12.
当n≥2时,an-an-1=2n,an-1-an-2=2(n-1),…,a3-a2=2×3,a2-a1=2×2,
累加可得:an-a1=2[n+(n-1)+…+3+2],
∴${a}_{n}=2[n+(n-1)+…+2+1]=2×\frac{n(n+1)}{2}=n(n+1)$.
当n=1时,a1=2满足上式,
∴an=n(n+1);
(Ⅱ)bn=$\frac{1}{{a}_{n+1}}$+$\frac{1}{{a}_{n+2}}$+$\frac{1}{{a}_{n+3}}$+…+$\frac{1}{{a}_{2n+1}}$
=$\frac{1}{(n+1)(n+2)}+\frac{1}{(n+2)(n+3)}+…+$$\frac{1}{(2n+1)(2n+2)}$
=$\frac{1}{n+1}-\frac{1}{n+2}+\frac{1}{n+2}-\frac{1}{n+3}+…+\frac{1}{2n+1}-\frac{1}{2n+2}$
=$\frac{1}{n+1}-\frac{1}{2n+2}=\frac{1}{2(n+1)}$.
即当n=1时,$({b}_{n})_{max}=\frac{1}{4}$.
∴若bn≤m恒成立,则实数m的取值范围为[$\frac{1}{4},+∞$).
点评 本题考查数列递推式,训练了累加法求数列的通项公式,考查裂项相消法求数列的前n项和,是中档题.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | [1,e+$\frac{1}{e}$] | B. | [1,e-$\frac{1}{e}$] | C. | [e-$\frac{1}{e}$,e+$\frac{1}{e}$] | D. | [e-$\frac{1}{e}$,e] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{4}}]$ | B. | $({\frac{1}{4},\frac{1}{2}}]$ | C. | $[{\frac{1}{4},\frac{1}{2}})$ | D. | $({0,\frac{1}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
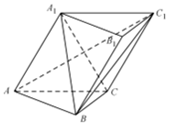 如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,底面ABC是等腰直角三角形,CA=CB,A1B⊥AC1.
如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,底面ABC是等腰直角三角形,CA=CB,A1B⊥AC1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2-i}{5}$ | B. | $\frac{2+i}{5}$ | C. | $\frac{1-2i}{5}$ | D. | $\frac{1+2i}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com