
分析 (Ⅰ)分类讨论化简f(x)的解析式,由f(x)的单调性及f(-3)=f(2)=5,得f(x)≤5 的解集.
(Ⅱ)由f(x)=$\left\{\begin{array}{l}{-(a+1)x-1,x≤-2}\\{(1-a)x+3,-2<x<\frac{1}{a}}\\{(a+1)x+1,x≥\frac{1}{a}}\end{array}\right.$ 的单调性,以及f(x)的图象连续不断,可得要是f(x)≥2,当且仅当f(-2)≥2,且f($\frac{1}{a}$)≥2,由此求得a的最小值.
解答 解:(Ⅰ)若a=1,f(x)=$\left\{\begin{array}{l}{-2x-1,x≤-2}\\{3,-2<x≤1}\\{2x+1,x>1}\end{array}\right.$,
由f(x)的单调性及f(-3)=f(2)=5,得f(x)≤5 的解集为{x|-3≤x≤2}.
(Ⅱ)f(x)=$\left\{\begin{array}{l}{-(a+1)x-1,x≤-2}\\{(1-a)x+3,-2<x<\frac{1}{a}}\\{(a+1)x+1,x≥\frac{1}{a}}\end{array}\right.$,
当x∈(-∞,-2]时,f(x)单调递减;当x∈[$\frac{1}{a}$,+∞)时,f(x)单调递增,
又f(x)的图象连续不断,所以f(x)≥2,当且仅当f(-2)=2a+1≥2,且f($\frac{1}{a}$)=$\frac{1}{a}$+2≥2,
求得a≥$\frac{1}{2}$,故a的最小值为$\frac{1}{2}$.
点评 本题主要考查绝对值不等式的解法,函数的单调性的应用,函数的恒成立问题,体现了转化、分类讨论的数学思想,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [15°,90°] | B. | [60°,90°] | C. | [15°,105°] | D. | [30°,105°] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}$>$\frac{1}{b}$ | B. | a2<b2 | C. | a2b<ab2 | D. | a3<b3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
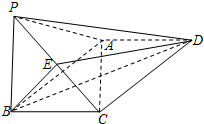 如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com