已知函数f(x)对任意的x,y∈R,总有f(x)+f(y)=f(x+y),且x<0时,f(x)>0.
(1)求证:函f(x)是奇函数;
(2)求证:函数f(x)是R上的减函数;
(3)若定义在(-2,2)上的函数f(x)满足f(-m)+f(1-m)<0,求实数m的取值范围.
【答案】
分析:(1)由f(x+y)=f(x)+f(y)可令x=y=0 有f (0 )=0,令y=-x 代入即证;
(2)设x
2>x
1则x
1-x
2<0,由已知当x<0时,f(x)>0可得f(x
1-x
2)>0,则f(x
1)=f[(x
1-x
2)+x
2]=f(x
1-x
2)+f(x
2)>f(x
2)可证;
(3)移项,利用奇偶性进行化简,然后利用单调性建立不等式,注意定义域,从而可求出m的取值范围.
解答:(1)证明:∵f(x+y)=f(x)+f(y)
∴令x=y=0 有f (0 )=0
令y=-x 有:0=f(0)=f(x+(-x))=f(x)+f(-x)
∴函数f(x)是奇函数;…(5分)
(2)证明:设x
2>x
1则x
1-x
2<0
∵当x<0时,f(x)>0
∴f(x
1-x
2)>0
∴f(x
1)=f[(x
1-x
2)+x
2]=f(x
1-x
2)+f(x
2)>f(x
2)
∴函数f(x)是R上的减函数
(3)解:∵f(-m)+f(1-m)<0,∴f(-m)<f(m-1),
且f(-m)+f(1-m)=f(1-2m)
∴
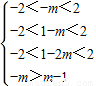
,解得:-

<m<

.…(16分)
点评:本题主要考查了利用赋值法求解抽象函数函数值,及利用赋值判断函数的奇偶性,利用函数单调性求解函数的最值,利用构造条件判断抽象函数的单调性的技巧要求体会掌握,是函数知识的综合应用,属于中档题.

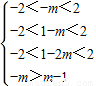 ,解得:-
,解得:- <m<
<m< .…(16分)
.…(16分)

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案