
 为数列
为数列 的前
的前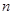 项和,
项和,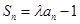 (
( 为常数且
为常数且 ,
, ).
).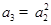 ,求
,求 的值;
的值; ,数列
,数列 满足
满足 ,且
,且 .若不等式
.若不等式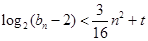 对任意
对任意 恒成立,求实数
恒成立,求实数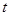 的取值范围.
的取值范围.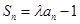 ,
,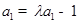 ,
,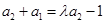 ,
,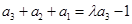 .………4分
.………4分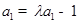 可知:
可知: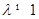 .
. 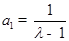 ,
, ,
,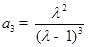 .
.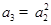 , 所以
, 所以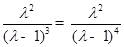 .
.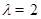 . ……7分
. ……7分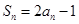 , 所以
, 所以 .
.  ,即
,即 .…………9分
.…………9分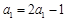 ,即
,即 . 可得:
. 可得: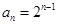 . ………10分
. ………10分 ,且
,且 ,
,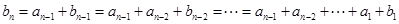
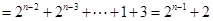 . ……………12分
. ……………12分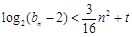 对任意
对任意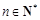 恒成立,
恒成立,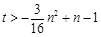 对任意
对任意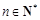 恒成立. ……………13分
恒成立. ……………13分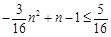 ,且
,且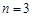 时,
时,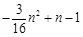 取得最大值
取得最大值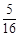 ,
,  . 所以
. 所以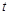 的取值范围是
的取值范围是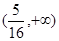 . ………15分
. ………15分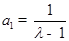 ,进而求出
,进而求出 ,
,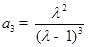 ,再根据
,再根据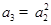 ,建立关于
,建立关于 的方程求解即可.
的方程求解即可.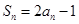 ,然后根据此式,可求得
,然后根据此式,可求得 ,从而求出
,从而求出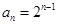 ,
,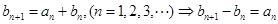 采用叠加的方法求得
采用叠加的方法求得 ,
,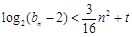 对任意
对任意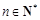 恒成立转化为
恒成立转化为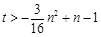 对任意
对任意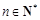 恒成立的常规问题解决.
恒成立的常规问题解决.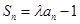 ,
,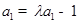 ,
,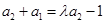 ,
,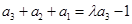 .………4分
.………4分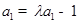 可知:
可知: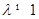 .
. 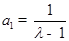 ,
, ,
,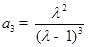 .
.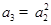 , 所以
, 所以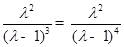 .
.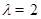 . ……7分
. ……7分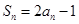 , 所以
, 所以 .
.  ,即
,即 .…………9分
.…………9分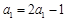 ,即
,即 . 可得:
. 可得: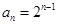 . ………10分
. ………10分 ,且
,且 ,
,
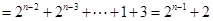 . ……………12分
. ……………12分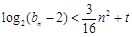 对任意
对任意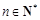 恒成立,
恒成立,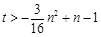 对任意
对任意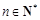 恒成立. ……………13分
恒成立. ……………13分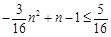 ,且
,且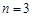 时,
时,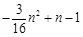 取得最大值
取得最大值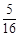 ,
,  . 所以
. 所以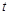 的取值范围是
的取值范围是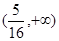 . ………15分
. ………15分

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
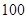 万元进行科研、技术改造与广告投入,方能保持原有的利润增长率.设经过
万元进行科研、技术改造与广告投入,方能保持原有的利润增长率.设经过 年后该项目的资金为
年后该项目的资金为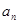 万元.
万元.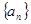 的前三项
的前三项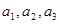 ,并猜想写出通项
,并猜想写出通项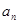 .
. 千万元.
千万元.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
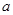 、
、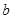 、
、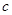 成等差数列,则
成等差数列,则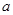 、
、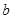 、
、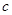 之比为
之比为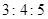 ;
;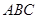 的三内角
的三内角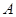 、
、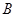 、
、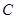 成等差数列,则
成等差数列,则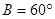 ;
;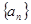 的前
的前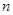 项和为
项和为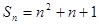 ,则
,则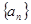 的通项公式
的通项公式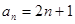 ;
;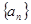 的前
的前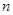 项和为
项和为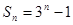 ,则
,则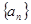 为等比数列。
为等比数列。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com