
 如图,圆O是△ABC的外接圆,∠BAC的平分线交BC于点F,D是AF的延长线与⊙O的交点,AC的延线与⊙O的切线DE交于点E.
如图,圆O是△ABC的外接圆,∠BAC的平分线交BC于点F,D是AF的延长线与⊙O的交点,AC的延线与⊙O的切线DE交于点E.| CE |
| BD |
| DE |
| AD |
| 2 |
| CE |
| BD |
| DE |
| AD |
| 2 |
 (1)证明:连接CD,则
(1)证明:连接CD,则 |
| BD |
 |
| CD |
| CE |
| BD |
| DE |
| AD |
 |
| BD |
 |
| CD |
| 2 |
| 2 |
| BF |
| DC |
| BD |
| DE |
| BD•DC |
| DE |
| 9 |
| 2 |


科目:高中数学 来源: 题型:
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:
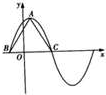 已知函数f(x)=
已知函数f(x)=| 3 |
| ωx |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
8
| ||
| 5 |
| 10 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 成绩分组 | 频数 | 频率 | 平均分 |
| [0,20) | 3 | 0.015 | 16 |
| [20,40) | a | b | 32.1 |
| [40,60) | 25 | 0.125 | 55 |
| [60,80) | c | 0.5 | 74 |
| [80,100] | 62 | 0.31 | 88 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com