
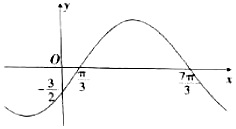
 已知函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示,将函数y=f(x)的图象向左平移$\frac{4π}{3}$个单位,得到函数y=g(x)的图象,则函数y=g(x)在区间$[{\frac{π}{2},\frac{5π}{2}}]$上的最大值为( )
已知函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示,将函数y=f(x)的图象向左平移$\frac{4π}{3}$个单位,得到函数y=g(x)的图象,则函数y=g(x)在区间$[{\frac{π}{2},\frac{5π}{2}}]$上的最大值为( )| A. | 3 | B. | $\frac{{3\sqrt{3}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
分析 利用函数的图象求出T,利用周期公式求出ω,利用函数的图象经过的特殊点,集合φ的范围,求出φ得到函数的解析式,进而可求g(x)解析式,利用正弦函数的性质即可得解.
解答 解:由图象可知T=4π,从而ω=$\frac{1}{2}$,
将($\frac{π}{3}$,0),(0,-$\frac{3}{2}$)在函数图象上,$\left\{\begin{array}{l}{Asin(\frac{π}{6}+φ)=0}\\{Asinφ=-\frac{3}{2}}\end{array}\right.$,|φ|<$\frac{π}{2}$,
可得:φ=-$\frac{π}{6}$,A=3,f(x)=3sin($\frac{1}{2}x$-$\frac{π}{6}$),
可得:g(x)=3sin[$\frac{1}{2}$(x+$\frac{4π}{3}$)-$\frac{π}{6}$]=3cos$\frac{1}{2}x$.
由x∈$[{\frac{π}{2},\frac{5π}{2}}]$,可得:$\frac{1}{2}x$∈[$\frac{π}{4}$,$\frac{5π}{4}$],
可得:3cos$\frac{1}{2}x$∈[-3,$\frac{3\sqrt{2}}{2}$].
故选:C.
点评 本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换,考查计算能力,属于基础题.


 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:选择题
| A. | 14 | B. | 15 | C. | 14或15 | D. | 15或16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
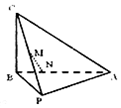 如图,在三棱锥C-PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,点M是PC的中点,点N在线段AB上,且MN⊥AB.
如图,在三棱锥C-PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,点M是PC的中点,点N在线段AB上,且MN⊥AB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
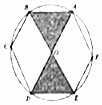 已知正六边形ABCDEF内接于圆O,连接AD,BE,现在往圆O内投掷2000粒小米,则可以估计落在阴影区域内的小米的粒数大致是( )(参考数据:$\frac{π}{\sqrt{3}}$=1.82,$\frac{\sqrt{3}}{π}$=0.55)
已知正六边形ABCDEF内接于圆O,连接AD,BE,现在往圆O内投掷2000粒小米,则可以估计落在阴影区域内的小米的粒数大致是( )(参考数据:$\frac{π}{\sqrt{3}}$=1.82,$\frac{\sqrt{3}}{π}$=0.55)| A. | 550 | B. | 600 | C. | 650 | D. | 700 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1] | B. | (-∞,-1] | C. | [-1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
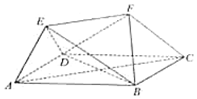 如图,在多面体ABCDEF中,底面ABCD是菱形,AB=2,∠DAB=60°,EF∥AC,EF=$\sqrt{3}$.
如图,在多面体ABCDEF中,底面ABCD是菱形,AB=2,∠DAB=60°,EF∥AC,EF=$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com