
【题目】某家用电器公司生产一新款热水器,首先每年需要固定投入 200万元,其次每生产1百台,需再投入0.9万元.假设该公司生产的该款热水器当年能全部售出,但每销售1百台需另付运输费0.1万元.根据以往的经验,年销售总额![]() (万元)关于年产量
(万元)关于年产量![]() (百台)的函数为
(百台)的函数为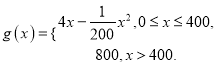 .
.
(1)将年利润![]() 表示为年产量
表示为年产量![]() 的函数;
的函数;
(2)求该公司生产的该款热水器的最大年利润及相应的年产量.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
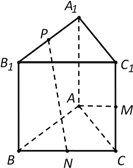
【题目】如图,直三棱柱ABC-A1B1C1中, AB=AC=AA1,AB⊥AC,M是CC1的中点,N是BC的中点,点P在线段A1B1上运动.
(Ⅰ)求证:PN⊥AM;
(Ⅱ)试确定点P的位置,使直线PN和平面ABC所成的角
最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修![]() :不等式选讲
:不等式选讲
已知函数f(x)=|2x+3|+|2x﹣1|.
(Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若关于x的不等式f(x)≤|3m+1|有解,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com