
设等差数列{an}的前n项和为Sn,则S4,S8-S4,S12-S8,S16-S12成等差数列.类比以上结论有:设等比数列{bn}的前n项积为Tn,则T4,________,________,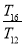 成等比数列.
成等比数列.
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-4直线、平面平行的判定及性质(解析版) 题型:填空题
过三棱柱ABC-A1B1C1的任意两条棱的中点作直线,其中与平面ABB1A1平行的直线共有________条.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-7数学归纳法(解析版) 题型:填空题
用数学归纳法证明不等式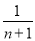 +
+ +…+
+…+ >
> 的过程中,由n=k推导n=k+1时,不等式的左边增加的式子是________.
的过程中,由n=k推导n=k+1时,不等式的左边增加的式子是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-6直接证明与间接证明(解析版) 题型:选择题
用反证法证明某命题时,对结论:“自然数a,b,c中恰有一个偶数”正确的反设为( )
A.a,b,c中至少有两个偶数
B.a,b,c中至少有两个偶数或都是奇数
C.a,b,c都是奇数
D.a,b,c都是偶数
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-5合情推理与演绎推理(解析版) 题型:填空题
如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行,依此类推,则(1)按网络运作顺序第n行第1个数字(如第2行第1个数字为2,第3行第1个数字为4,…)是________;(2)第63行从左至右的第4个数字应是________.
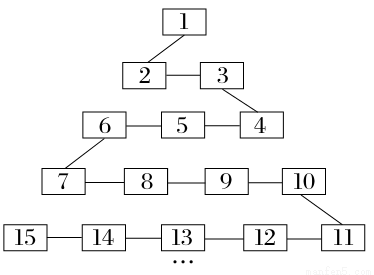
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-5合情推理与演绎推理(解析版) 题型:选择题
三段论推理“①矩形是平行四边形;②三角形不是平行四边形;③三角形不是矩形”中的小前提是( )
A.① B.② C.③ D.①和②
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-4基本不等式(解析版) 题型:解答题
已知A、B、C是平面上任意三点,BC=a,CA=b,AB=c,求y=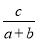 +
+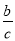 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-2一元二次不等式及其解法(解析版) 题型:填空题
已知函数f(x)=x2+ax-1在区间[0,3]上有最小值-2,则实数a的值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-4数列求和(解析版) 题型:解答题
已知数列{an}的前n项和为Sn,a1=2.当n≥2时,Sn-1+1,an,Sn+1成等差数列.
(1)求证:{Sn+1}是等比数列;
(2)求数列{nan}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com