
分析 (1)由$\overrightarrow{a}∥\overrightarrow{b}$,根据平行向量的坐标关系以及两角差的正弦公式即可得出sinx=0,这样根据x的范围便可得出x的值;
(2)进行向量数量积的坐标运算,根据两角差的余弦公式便可得出f(x)=cosx,从而可以写出余弦函数的单调递减区间.
解答 解:(1)∵$\overrightarrow{a}$∥$\overrightarrow{b}$;
∴cos$\frac{3x}{2}$sin$\frac{x}{2}$-sin$\frac{3x}{2}$cos$\frac{x}{2}$=0,即sinx=0;
∵x∈[0,$\frac{π}{2}$];
∴x=0;
(2)f(x)=$\overrightarrow{a}•\overrightarrow{b}$=cos$\frac{3x}{2}$cos$\frac{x}{2}$+sin$\frac{3x}{2}$sin$\frac{x}{2}$=cosx;
∴f(x)的单调递减区间为[2kπ,2kπ+π],k∈Z.
点评 考查平行向量的坐标关系,以及两角和与差的正余弦公式,已知三角函数值求角,向量数量积的坐标运算,以及余弦函数的单调区间.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | $\frac{24}{5}$ | D. | $\frac{28}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
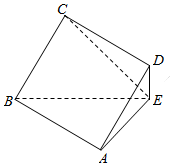 如图,四边形ABCD是正方形,DE⊥平面ABE,BE=3DE,DE=3,AB⊥AE.
如图,四边形ABCD是正方形,DE⊥平面ABE,BE=3DE,DE=3,AB⊥AE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com