练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．下列命题中，真命题的个数是（　　）
    ①经过直线外一点有且只有一条直线与已知直线平行
    ②经过直线外一点有且只有一条直线与已知直线垂直
    ③经过平面外一点有且只有一个平面与已知平面平行
    ④经过平面外一点有且只有一个平面与已知平面垂直．
    A．1个B．2个C．3个D．4个

    分析 在①，由平行公理得①是真命题；在②中，经过直线外一点有无数条直线与已知直线垂直；在③中，由面面平行的判定定理得③是真命题；在④中，经过平面外一点有无数个平面与已知平面垂直．

    解答 解：在①中：由平行公理得：经过直线外一点有且只有一条直线与已知直线平行，故①是真命题；
    在②中：经过直线外一点有无数条直线与已知直线垂直，故②是假命题；
    在③中：由面面平行的判定定理得经过平面外一点有且只有一个平面与已知平面平行，故③是真命题；
    在④中：经过平面外一点有无数个平面与已知平面垂直，故④是假命题．
    故选：B．

    点评 本题考查命题真假的判断，是中档题，解题时要认真审题，注意空间中线线、线面、面面间的位置关系的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    7．一汽车厂生产A，B，C三类轿车，每类轿车均有舒适型和标准型两种型号，某月的产量如下表（单位：辆）：
    轿车A轿车B轿车C
    舒适型100150z
    标准型300450600
    按类型分层抽样的方法在这个月生产的轿车中抽取50辆，其中有A类轿车10辆．
    （1）求z的值．
    （2）用分层抽样的方法在C类轿车中抽取一个容量为5的样本．将该样本看成一个总体，从中任取2辆，求至少有1辆舒适型轿车的概率；
    （3）用随机抽样的方法从B类舒适型轿车中抽取8辆，经检测它们的得分如下：9.4，8.6，9.2，9.6，8.7，9.3，9.0，8.2，求这8个数据的方差．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

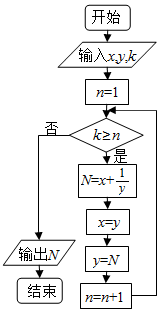
    8．执行如图所示的程序框图，若输入的x，y，k分别为1，2，3，则输出的N=（　　）
    A．$\frac{3}{2}$B．$\frac{15}{8}$C．$\frac{16}{5}$D．$\frac{8}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知函数f（x）=x2+mx+4．
    （Ⅰ）当x∈（1，2）时，不等式f（x）＜0恒成立，求实数m的取值范围；
    （Ⅱ）若不等式|$\frac{f（x）-{x}^{2}}{m}$|＜1的解集中的整数有且仅有1，2，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点（0，1），且离心率e=$\frac{\sqrt{3}}{2}$．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）已知直线l与椭圆C交于A（x1，y1），B（x2，y2）两点，且△OAB的面积为S，其中O为坐标原点，当S取得最大值时，求y${\;}_{1}^{2}$+y${\;}_{2}^{2}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．（x+1）2（$\frac{1}{x}$-1）5的展开式中常数项为（　　）
    A．21B．19C．9D．-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．（2x+$\frac{1}{x}$）n的展开式的第三项系数与第四项系数相等，则二项式系数之和为（　　）
    A．128B．36C．256D．512

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知向量$\overrightarrow a=（{cos\frac{3x}{2}，sin\frac{3x}{2}}），\overrightarrow b=（{cos\frac{x}{2}，sin\frac{x}{2}}）$．
    （1）已知$\overrightarrow a$∥$\overrightarrow b$且$x∈[{0，\frac{π}{2}}]$，求x；
    （2）若$f（x）=\overrightarrow a•\overrightarrow b$，写出f（x）的单调递减区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知函数$f（x）=（{e^x}-\frac{1}{e^x}）{x^3}$，若实数a满足f（log2a）+f（log0.5a）≤2f（1），则实数a的取值范围是（　　）
    A．$（-∞，\frac{1}{2}）∪（2，+∞）$B．$（-∞，\frac{1}{2}]∪[2，+∞）$C．$[\frac{1}{2}，2]$D．$（\frac{1}{2}，2）$

    查看答案和解析>>

    同步练习册答案