
| A. | $(-∞,\frac{1}{2})∪(2,+∞)$ | B. | $(-∞,\frac{1}{2}]∪[2,+∞)$ | C. | $[\frac{1}{2},2]$ | D. | $(\frac{1}{2},2)$ |
分析 可判函数f(x)为偶函数,且在[0,+∞)上是增函数,原不等式可化为|log2a|≤1,由对数函数的单调性可解.
解答 解:∵$f(x)=({e^x}-\frac{1}{e^x}){x^3}$,∴f(-x)=($\frac{1}{{e}^{x}}$-ex)(-x)3
=(ex-$\frac{1}{{e}^{x}}$)x3=f(x),∴f(x)为偶函数,
不等式f(log2a)+f(log0.5a)≤2f(1),
等价为f(log2a)+f(-log2a)≤2f(1),
即2f(log2a)≤2f(1),即f(log2a)≤f(1),
又当x>0时f′(x)=(ex+$\frac{1}{{e}^{x}}$)x3+3(ex-$\frac{1}{{e}^{x}}$)x2>0
∴函数f(x)在[0,+∞)上是增函数,
∴不等式f(log2a)≤f(1)可化为|log2a|≤1,
即-1≤log2a≤1,由对数函数的单调性可得$\frac{1}{2}$≤a≤2,
故选:C.
点评 本题考查函数的单调性和导数的关系,涉及函数的奇偶性和对数的性质,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
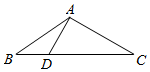 如图,已知点D在△ABC的BC边上,且∠DAC=90°,cosC=$\frac{\sqrt{6}}{3}$,AB=6,BD=$\sqrt{6}$,则ADsin∠BAD=.
如图,已知点D在△ABC的BC边上,且∠DAC=90°,cosC=$\frac{\sqrt{6}}{3}$,AB=6,BD=$\sqrt{6}$,则ADsin∠BAD=.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,1) | B. | (1,+∞) | C. | (1,2] | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
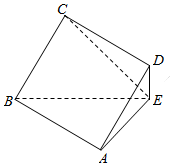 如图,四边形ABCD是正方形,DE⊥平面ABE,BE=3DE,DE=3,AB⊥AE.
如图,四边形ABCD是正方形,DE⊥平面ABE,BE=3DE,DE=3,AB⊥AE.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
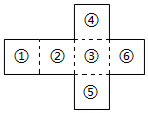 如图是一个正方体纸盒的展开图,把复数1,-1,2i,-2i,$\sqrt{2}$,-$\sqrt{2}$按虚线分别填入六个正方折成正方体后,相对面上的两个数的模相等,则不同的填法有48种(用数字作答)
如图是一个正方体纸盒的展开图,把复数1,-1,2i,-2i,$\sqrt{2}$,-$\sqrt{2}$按虚线分别填入六个正方折成正方体后,相对面上的两个数的模相等,则不同的填法有48种(用数字作答)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com