
| A. | 4 | B. | 5 | C. | $\frac{24}{5}$ | D. | $\frac{28}{5}$ |
分析 正实数m、n满足3m+4n=5mn,可得$\frac{4}{m}+\frac{3}{n}$=5.于是m+3n=$\frac{1}{5}(\frac{4}{m}+\frac{3}{n})$(m+3n),展开利用基本不等式的性质即可得出.
解答 解:∵正实数m、n满足3m+4n=5mn,
∴$\frac{4}{m}+\frac{3}{n}$=5.
则m+3n=$\frac{1}{5}(\frac{4}{m}+\frac{3}{n})$(m+3n)=$\frac{1}{5}$$(13+\frac{12n}{m}+\frac{3m}{n})$≥$\frac{1}{5}(13+2×3×\sqrt{\frac{4n}{m}•\frac{m}{n}})$=$\frac{1}{5}(13+12)$=5,当且仅当m=2n=2时取等号.
∴m+3n的最小值是5.
故选:B.
点评 本题考查了基本不等式的性质,考查了推理能力与计算能力,属于中档题.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:解答题
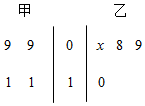 从甲、乙两个班级分别抽取4名同学的年龄制作出如右图所示的茎叶图,乙班的记录中有一个数据模糊,无法确认,在图中以X表示,已知这8个同学的平均年龄是9.5岁.
从甲、乙两个班级分别抽取4名同学的年龄制作出如右图所示的茎叶图,乙班的记录中有一个数据模糊,无法确认,在图中以X表示,已知这8个同学的平均年龄是9.5岁.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 128 | B. | 36 | C. | 256 | D. | 512 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com