
分析 先求其反函数,再根据三角形的性质即可求出值域.
解答 解:y=$\frac{1-cosx}{sinx+2}$
∴ysinx+2y=1-cosx,
∴ysinx+cosx=1-2y,
∴$\sqrt{1+{y}^{2}}$sin(x+θ)=1-2y,其中tanθ=$\frac{1}{\sqrt{1+{y}^{2}}}$
∴sin(x+θ)=$\frac{1-2y}{\sqrt{1+{y}^{2}}}$,
∵x∈[0,2π),
∴x+θ∈(θ,2π+θ)
∴-1≤sin(x+θ)≤1,
∴-1≤$\frac{1-2y}{\sqrt{1+{y}^{2}}}$≤1,
解得0≤y≤$\frac{4}{3}$
即函数的值域为[0,$\frac{4}{3}$].
点评 本题考查了函数的值域的求法,以及三角函数的性质,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | $\frac{24}{5}$ | D. | $\frac{28}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,1) | B. | (1,+∞) | C. | (1,2] | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
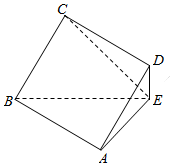 如图,四边形ABCD是正方形,DE⊥平面ABE,BE=3DE,DE=3,AB⊥AE.
如图,四边形ABCD是正方形,DE⊥平面ABE,BE=3DE,DE=3,AB⊥AE.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com