
【题目】近期,某市公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用![]() 表示活动推出的天数,
表示活动推出的天数, ![]() 表示每天使用扫码支付的人次(单位:十人次),统计数据如表1所示:
表示每天使用扫码支付的人次(单位:十人次),统计数据如表1所示:

根据以上数据,绘制了散点图.
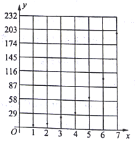
(1)根据散点图判断,在推广期内,![]() 与
与![]() (
(![]() 均为大于零的常数)哪一个适宜作为扫码支付的人次
均为大于零的常数)哪一个适宜作为扫码支付的人次![]() 关于活动推出天数
关于活动推出天数![]() 的回归方程类型?(给出判断即可,不必说明理由);
的回归方程类型?(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表1中的数据,建立![]() 关于
关于![]() 的回归方程,并预测活动推出第8天使用扫码支付的人次;
的回归方程,并预测活动推出第8天使用扫码支付的人次;
(3)推广期结束后,车队对乘客的支付方式进行统计,结果如下
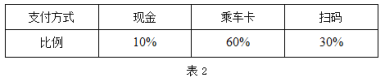
已知该线路公交车票价为2元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受8折优惠,扫码支付的乘客随机优惠,根据统计结果得知,使用扫码支付的乘客中有![]() 的概率享受
的概率享受![]() 折优惠,有
折优惠,有![]() 的概率享受8折优惠,有
的概率享受8折优惠,有![]() 的概率享受9折优惠.根据所给数据以事件发生的频率作为相应事件发生的概率,试估计从20名乘客从中随机抽取1人,恰好享受8折优惠的概率 .
的概率享受9折优惠.根据所给数据以事件发生的频率作为相应事件发生的概率,试估计从20名乘客从中随机抽取1人,恰好享受8折优惠的概率 .
参考数据:
|
|
|
|
|
66 | 1.54 | 2711 | 50.12 | 3.47 |
其中![]() ,
,![]()
参考公式:
对于一组数据![]()
![]()
![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: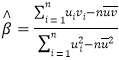 ,
,![]() .
.
【答案】(1)![]() 适宜作为扫码支付的人数
适宜作为扫码支付的人数![]() 关于活动推出天数
关于活动推出天数![]() 的回归方程类型;(2)3470;(3)
的回归方程类型;(2)3470;(3)![]() .
.
【解析】
(1)根据散点图直接写出结果即可;
(2)对![]() 两边同时取常用对数,得到
两边同时取常用对数,得到![]() ,设
,设![]() ,
,
得到![]() ,根据题中数据求出
,根据题中数据求出![]() ,
,![]() ,进而可得
,进而可得![]() ,再化简整理即可得出回归方程;将
,再化简整理即可得出回归方程;将![]() 代入所求回归方程即可求出预测值;
代入所求回归方程即可求出预测值;
(3)由题意确定享受八折优惠的人数,根据古典概型的概率计算公式即可求出结果.
(1)根据散点图判断,![]() 适宜作为扫码支付的人数
适宜作为扫码支付的人数![]() 关于活动推出天数
关于活动推出天数![]() 的回归方程类型;
的回归方程类型;
(2)∵![]() ,两边同时取常用对数得:
,两边同时取常用对数得:![]() ;设
;设![]() ∵
∵
∴![]() ,∵
,∵![]() ,
,
∴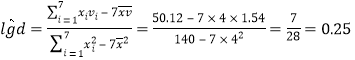 ,
,
把样本中心点![]() 代入
代入![]() ,得:
,得:![]() ,∴
,∴![]() ,
,
∴![]() ,∴y关于x的回归方程式:
,∴y关于x的回归方程式:![]() ;
;
把![]() 代入上式: ∴
代入上式: ∴![]() ;
;
活动推出第8天使用扫码支付的人次为3470;
(3)由题意,20名乘客中,现金支付的有2人,乘车卡支付的有12人,扫码支付的有6人,
其中享受八折优惠的共有,12+2=14人,由古典概型计算公式,所以估计从20名乘客从中随机抽取1人,恰好享受8折优惠的概率为![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:
【题目】某网站从春节期间参与收发网络红包的手机用户中随机抽取![]() 名进行调查,将受访用户按年龄分成
名进行调查,将受访用户按年龄分成![]() 组:
组: ![]() ,
, ![]() ,…,
,…, ![]() ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图:

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)从春节期间参与收发网络红包的手机用户中随机抽取一人,估计其年龄低于![]() 岁的概率;
岁的概率;
(Ⅲ)估计春节期间参与收发网络红包的手机用户的平均年龄.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解本校学生网课期间课后玩电脑游戏时长情况,随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生每天玩电脑游戏的时长的频率分布直方图.
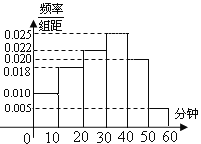
(1)根据频率分布直方图估计抽取样本的平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)已知样本中玩电脑游戏时长在![]() 的学生中,男生比女生多1人,现从中任选3人进行回访,求选出的3人中恰有两人是男生的概率.
的学生中,男生比女生多1人,现从中任选3人进行回访,求选出的3人中恰有两人是男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某一部件由四个电子元件按如图方式连接而成,元件1或元件2正常工作,且元件3或元件4正常工作,则部件正常工作.设四个电子元件的使用寿命(单位:小时)均服从正态分布![]() ,且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为__________.
,且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是两条不同的直线,
是两条不同的直线,![]() ,
,![]() ,
,![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,
,![]() ,则
,则![]()
②若![]() ,
,![]() ,
,![]() ,则
,则![]()
③若![]() ,
,![]() ,则
,则![]()
④若![]() ,
,![]() ,则
,则![]()
其中正确命题的序号是( )
A.①和②B.②和③C.③和④D.①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是函数![]() 的导函数
的导函数![]() 的图象,给出下列命题:
的图象,给出下列命题:
①-2是函数![]() 的极值点;
的极值点;
②1是函数![]() 的极值点;
的极值点;
③![]() 的图象在
的图象在![]() 处切线的斜率小于零;
处切线的斜率小于零;
④函数![]() 在区间
在区间![]() 上单调递增.
上单调递增.
则正确命题的序号是( )

A. ①③ B. ②④ C. ②③ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学学生会为了调查爱好游泳运动与性别是否有关,通过随机询问110名性别不同的高中生是否爱好游泳运动得到如下的列联表:
p(k2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由![]() ,并参照附表,得到的正确结论是( )
,并参照附表,得到的正确结论是( )
A. 在犯错误的概率不超过![]() 的前提下,认为“爱好游泳运动与性别有关”
的前提下,认为“爱好游泳运动与性别有关”
B. 在犯错误的概率不超过![]() 的前提下,认为“爱好游泳运动与性别无关”
的前提下,认为“爱好游泳运动与性别无关”
C. 有![]() 的把握认为“爱好游泳运动与性别有关”
的把握认为“爱好游泳运动与性别有关”
D. 有![]() 的把握认为“爱好游泳运动与性别无关”
的把握认为“爱好游泳运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】机床厂今年年初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y万元.
(Ⅰ)写出y与x之间的函数关系式;
(Ⅱ)从第几年开始,该机床开始盈利(盈利额为正值);
(Ⅲ)使用若干年后,对机床的处理方案有两种:
(1)当年平均盈利额达到最大值时,以30万元价格处理该机床;
(2)当盈利额达到最大值时,以12万元价格处理该机床.
请你研究一下哪种方案处理较为合理?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市交通部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照![]() 分成5组,制成如图所示频率分直方图.
分成5组,制成如图所示频率分直方图.
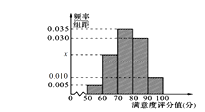
(1)求图中x的值;
(2)求这组数据的平均数和中位数;
(3)已知满意度评分值在![]() 内的男生数与女生数3:2,若在满意度评分值为
内的男生数与女生数3:2,若在满意度评分值为![]() 的人中随机抽取2人进行座谈,求2人均为男生的概率.
的人中随机抽取2人进行座谈,求2人均为男生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com